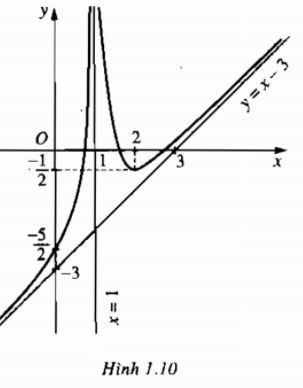
Câu 1.37 trang 17 sách bài tập Giải tích 12 Nâng caoTìm tiệm cận đứng và tiệm cận xiên của đồ thị các hàm số sau: Tìm tiệm cận đứng và tiệm cận xiên của đồ thị các hàm số sau: a) \(y = 2x - 1 + {1 \over x}\) b) \(y = {{{x^2} + 2x} \over {x - 3}}\) c) \(y = x - 3 + {1 \over {2{{(x - 1)}^2}}}\) d) \(y = {{2{x^2} + {x^2}} \over {{x^2} + 1}}\) Giải a) Đường thẳng x = 0 là tiệm cận đứng của đồ thị (khi \(x \to {0^ + }\) và \(x \to {0^ - }\). Đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)) b) Đường thẳng x = 3 là tiệm cận đứng của đồ thị (khi \(x \to {3^ - }\) và \(x \to {3^ + }\)). Đường thẳng y = x + 5 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)) c) Vì \(\mathop {\lim }\limits_{x \to 1} y = + \infty \) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị (khi \(x \to {1^ - }\) và \(x \to {1^ + }\)). Vì \(y - (x - 3) = {1 \over {2{{(x - 1)}^2}}} \to 0\) khi \(x \to + \infty \) và \(x \to - \infty \) nên đường thẳng y = x – 3 là tiệm cân xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)) (h.1.10).
d) Đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)) Có thể viết hàm số đã cho dưới dạng \(y = 2x - 1 + {{1 - 2x} \over {{x^2} + 1}} \) Vì hàm số xác định trên R nên đồ thị của nó không có tiệm cận đứng. Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 5. Đường tiệm cận của hàm số
|
-
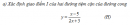
Câu 1.40 trang 18 sách bài tập Giải tích 12 Nâng cao
a) Xác định giao điểm I của hai đường tiệm cận của đường cong
-
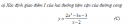
Câu 1.41 trang 18 sách bài tập Giải tích 12 Nâng cao
a) Xác định giao điểm I của hai đường tiệm cận của đường cong

 Tải ngay
Tải ngay