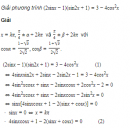Câu 1.45 trang 15 sách bài tập Đại số và Giải tích 11 Nâng cao

Tìm các nghiệm của phương trình trên khoảng \(\left( {{\pi  \over 4};{{5\pi } \over 4}} \right)\) rồi tìm giá trị gần đúng của chúng, chính xác đến hàng phần trăm:

           \(\cos x + \sin x + {1 \over {\sin x}} + {1 \over {\cos x}} = {{10} \over 3}\)

Giải

Ta có:      \(\cos x + \sin x + {1 \over {\sin x}} + {1 \over {\cos x}} = {{10} \over 3}\)

               \( \Leftrightarrow \cos x + \sin x + {{\sin x + \cos x} \over {\sin x\cos x}} = {{10} \over 3}\)

Đặt \(t = \cos x + \sin x\)  với \(\left| t \right| \le \sqrt 2 .\) Khi đó \(\sin x\cos x = {{{t^2} - 1} \over 2}\) và phương trình trở thành

                \(t + {{2t} \over {{t^2} - 1}} = {{10} \over 3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)

Với điều kiện \(t \ne  \pm 1,\) ta có:

\((1) \Leftrightarrow 3{t^2} - 10{t^2} + 3t + 10 = 0\)

\(\Leftrightarrow \left( {t - 2} \right)\left( {3{t^2} - 4t - 5} \right) = 0\)

Phương trình này có ba nghiệm \({t_1} = 2,{t_2} = {{2 + \sqrt {19} } \over 3}\) và \({t_3} = {{2 - \sqrt {19} } \over 3}.\)

Tuy nhiên, chỉ có \({t_3} = {{2 - \sqrt {19} } \over 3}\) là thỏa mãn điều kiện \(\left| t \right| \le \sqrt 2 .\) Do đó phương trình đa cho tương đương với \(\cos x + \sin x = {{2 - \sqrt {19} } \over 3}\) hay

              \(\cos \left( {x - {\pi  \over 4}} \right) = {{2 - \sqrt {19} } \over {3\sqrt 2 }}\,\,\,\,\,\,\,\,\,(2)\)

Điều kiện  \({\pi  \over 4} < x < {{5\pi } \over 4}\) tương đương với điều kiện \(0 < x   - {\pi  \over 4} < \pi .\) Với điều kiện đó ta có

\((2) \Leftrightarrow x - {\pi  \over 4} = \arccos {{2 - \sqrt {19} } \over {3\sqrt 2 }}\)

       \(\Leftrightarrow x = {\pi  \over 4} + \arccos {{2 - \sqrt {19} } \over {3\sqrt 2 }}\)

Lấy các giá trị gần đúng \({\pi  \over 4} \approx 0,785\) và \(\arccos {{2 - \sqrt {19} } \over {3\sqrt 2 }} \approx 2,160\) ta được \(x \approx 2,95.\)

sachbaitap.com