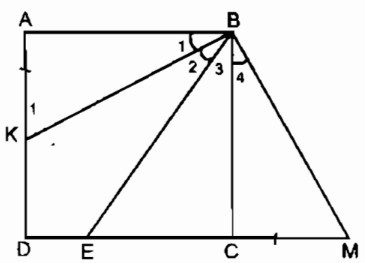
Câu 154 trang 99 Sách bài tập (SBT) Toán 8 tập 1Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK + CE = BE. Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK + CE = BE. Giải:
Trên tia đối tia CD lấy điểm M sao cho CM = AK Ta có: AK + CE = CM + CE = EM (*) Xét ∆ ABK và ∆ CBM: AB = CB (gt) \(\widehat A = \widehat C = {90^0}\) AK = CM (theo cách vẽ) Do đó: ∆ ABK = ∆ CBM (c.g.c) \( \Rightarrow {\widehat B_1} = {\widehat B_4}\) (1) \(\widehat {KBC} = {90^0} - {\widehat B_1}\) (2) Trong tam giác CBM vuông tại C. \(\widehat M = {90^0} - {\widehat B_4}\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {KBC} = \widehat M\) (4) \(\widehat {KBC} = {\widehat B_2} + {\widehat B_3}\) mà \({\widehat B_1} = {\widehat B_2}\) (gt) \({\widehat B_1} = {\widehat B_4}\) (chứng minh trên) Suy ra: \({\widehat B_2} = {\widehat B_4} \Rightarrow {\widehat B_2} + {\widehat B_3} = {\widehat B_3} + {\widehat B_4}\) hay \(\widehat {KBC} = \widehat {EBM}\) (5) Từ (4) và (5) suy ra: \(\widehat {EBM} = \widehat M\) ⇒ ∆ EBM cân tại E ⇒ EM = BE (**) Từ (*) và (**) suy ra: AK + CE = BE. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 12. Hình vuông
|
-
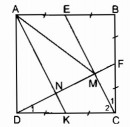
Câu 155 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. a. Chứng minh rằng CE vuông góc với DF

 Tải ngay
Tải ngay