Câu 159 trang 100 Sách bài tập (SBT) Toán 8 tập 1Chứng minh rằng D đối xứng với E qua A Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC. a. Chứng minh rằng D đối xứng với E qua A b. Tam giác DHE là tam giác gì ? Vì sao ? c. Tứ giác BDEC là hình gì ? Vì sao ? d. Chứng minh rằng BC = BD + CE. Giải:
a. Điểm D đối xứng điểm H qua trục AB ⇒ AB là đường trung trực của HD ⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A Suy ra: AB là tia phân giác của \(\widehat {DAH} \Rightarrow \widehat {DAB} = {\widehat A_1}\) Điểm H và điểm E đối xứng qua trục AC ⇒ AC là đường trung trực của HE ⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A Suy ra: AC là đường phân giác của \(\widehat {HAE} \Rightarrow {\widehat A_2} = \widehat {EAC}\) \(\widehat {DAE} = \widehat {DAH} + \widehat {HAE} = 2\left( {{{\widehat A}_1} + {{\widehat A}_2}} \right) = {2.90^0} = {180^0}\) D, A, E thẳng hàng AD = AE (vì cùng bằng AH) nên điểm A là trung điểm của đoạn DE Vậy điểm D đối xứng với điểm E qua điểm A. b) Tam giác DHE có HA là trung tuyến và \(AH = {1 \over 2}DE\)
+) AB chung +) BD = BH ( vì AB là trung trực của DH) +) AD = AH (vì AB là trung trực của DH) \(\Rightarrow \Delta ADB = \Delta AHB\;(c.c.c)\) \( \Rightarrow \widehat {AHB} = \widehat {ADB}=90^0\) (hai góc tương ứng) Xét \(\Delta AEC\) và \( \Delta AHC\) có: +) AC chung +) EC = HC ( vì AC là trung trực của EH) +) AE = AH (vì AC là trung trực của EH) \(\Rightarrow \Delta AEC = \Delta AHC\;(c.c.c)\) \( \Rightarrow \widehat {AHC} = \widehat {AEC}=90^0\) (hai góc tương ứng) Suy ra BD//CE (vì cùng vuông góc với DE) d) Do AB là đường trung trực của DH nên BD=BH (5) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài tập ôn chương I - Tứ giác
|
-
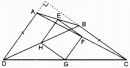
Câu 160 trang 100 Sách bài tập (SBT) Toán 8 tập 1
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:

 Tải ngay
Tải ngay