Tải ngay
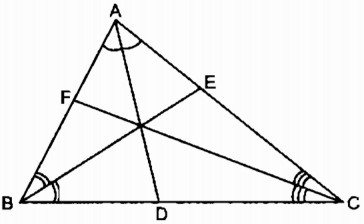
Câu 18 trang 87 Sách bài tập (SBT) Toán 8 tập 2Chứng minh rằng: Tam giác ABC có các đường phân giác AD, BE và CF Chứng minh rằng: \({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = 1\)
Giải: Trong tam giác ABC, ta có: AD là đường phân giác của \(\widehat {BAC}\) Suy ra: \({{DB} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác ) (1) BE là đường phân giác \(\widehat {ABC}\) Suy ra: \({{EC} \over {EA}} = {{BC} \over {AB}}\) (tính chất đường phân giác ) (2) CF là đường phân giác của \(\widehat {ACB}\) Suy ra: \({{FA} \over {FB}} = {{CA} \over {CB}}\) (tính chất đường phân giác ) (3) Nhân từng vế (1), (2) và (3), ta có: \({{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = {{AB} \over {AC}}.{{BC} \over {AB}}.{{CA} \over {CB}} = 1\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 3. Tính chất đường phân giác của tam giác
|
