Tải ngay
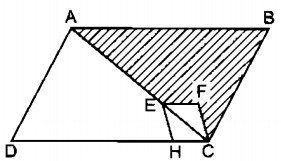
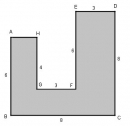
Câu 23 trang 158 Sách bài tập (SBT) Toán 8 tập 1Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích. Trên hình 185, các tứ giác ABCD và EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. a. Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích. b. ABCFE có phải là đa giác lồi không ? Vì sao ? Giải:
a. Ta có: ∆ ABC = ∆ CDA (c.c.c) \( \Rightarrow {S_{ABC}} = {S_{CDA}}\) (1) ∆ EFC = ∆ CHE (c.c.c) \( \Rightarrow {S_{EFC}} = {S_{CHE}}\) (2) Từ (1) và (2) suy ra: \({S_{ABC}} - {S_{EFC}} = {S_{CDA}} - {S_{CHE}}\) Hay \({S_{ABCFE}} = {S_{AEHD}}\) b. Hình ABCFE không phải đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 2. Diện tích hình chữ nhật
|
-
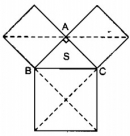
Câu 24 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền(không sử dụng định lý Py-ta-go)
-
Câu 2.1 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 33,33cm ?
