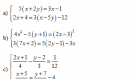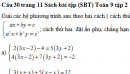Giải các hệ phương trình sau:
\(a)\left\{ {\matrix{
{8x - 7y = 5} \cr
{12x + 13y = - 8} \cr} } \right.\)
\(b)\left\{ {\matrix{
{3\sqrt 5 x - 4y = 15 - 2\sqrt 7 } \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr} } \right.\)
Giải
a)
\(\eqalign{
& \left\{ {\matrix{
{8x - 7y = 5} \cr
{12x + 13y = - 8} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{24x - 21y = 15} \cr
{24x + 26y = - 16} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{47y = - 31} \cr
{8x - 7y = 5} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - {{31} \over {47}}} \cr
{8x - 7.\left( { - {{31} \over {47}}} \right) = 5} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = - {{31} \over {47}}} \cr
{8x = 5 - {{217} \over {47}}} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - {{31} \over {47}}} \cr
{x = {9 \over {188}}} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( {{9 \over {188}}; - {{31} \over {47}}} \right)\)
b)
\(\eqalign{
& \left\{ {\matrix{
{3\sqrt 5 x - 4y = 15 - 2\sqrt 7 } \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{6\sqrt 5 x - 8y = 30 - 4\sqrt 7 } \cr
{ - 6\sqrt 5 x + 24\sqrt 7 y = 54} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{\left( {24\sqrt 7 - 8} \right)y = 84 - 4\sqrt 7 } \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = {{4\left( {21 - \sqrt 7 } \right)} \over {8\left( {3\sqrt 7 - 1} \right)}}} \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{\left( {21 - \sqrt 7 } \right)\left( {3\sqrt 7 + 1} \right)} \over {2.\left( {9.7 - 1} \right)}}} \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = {{62\sqrt 7 } \over {2.62}}} \cr
{ - 2\sqrt 5 x + 8\sqrt 7 y = 18} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{\sqrt 7 } \over 2}} \cr
{ - 2\sqrt 5 x + 8\sqrt 7 .{{\sqrt 7 } \over 2} = 18} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = {{\sqrt 7 } \over 2}} \cr
{ - 2\sqrt 5 x = - 10} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = {{\sqrt 7 } \over 2}} \cr
{x = {{10} \over {2\sqrt 5 }}} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = {{\sqrt 7 } \over 2}} \cr
{x = \sqrt 5 } \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm \((x; y) = \left( {\sqrt 5 ;{{\sqrt 7 } \over 2}} \right)\)
Sachbaitap.com

 Tải ngay
Tải ngay