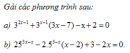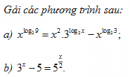Câu 2.97 trang 86 sách bài tập Giải tích 12 Nâng caoTìm m để mỗi phương trình sau có nghiệm duy nhất: Tìm m để mỗi phương trình sau có nghiệm duy nhất: a) \({16^{x + 1}} + {4^{x - 1}} - 5m = 0;\) b) \(2{\log _2}\left( {x + 4} \right) = {\log _2}\left( {mx} \right).\) Giải a) Đặt \({4^x} = t(t > 0)\). Bài toán trở thành: Tìm m để phương trình \(16{t^2} + {t \over 4} - 5m = 0\) (1) có nghiệm dương duy nhất. Điều kiện để (1) có nghiệm là \(\Delta = {1 \over {16}} + 320m \ge0\) hay \(m\ge - {1 \over {5120}}\) . Lại có \({t_1} + {t_2} = - {1 \over {64}};{t_1}{t_2} = - {{5m} \over {16}}\) . Nên (1) có nghiệm duy nhất khi \( - {{5m} \over {16}} < 0\), tức là m > 0. b) Bài toán quy về tìm m để hệ \(\left\{ \matrix{{(x + 4)^2} = mx \hfill \cr x + 4 > 0 \hfill \cr} \right.\) có nghiệm duy nhất hay \(\left\{ \matrix{{x^2} + (8 - m)x + 16 = 0\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \cr x > - 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2\right) \hfill \cr} \right.\) có nghiệm duy nhất tức là (1) có nghiệm duy nhất thỏa mãn \(x > - 4\). Phương trình (1) có nghiệm khi\(\Delta = {m^2} - 16m \ge 0\) hay \(m \le 0\) hoặc \(m \ge 16\) . Xét cả trường hợp : +) \(m = 0\) thì (1) có nghiệm kép \({x_1} = {x_2} = {{0 - 8} \over 2} = - 4\) ( không thỏa mãn \(x > - 4\) ). +) \(m = 16\) thì (1) có nghiệm kép \({x_1} = {x_2} = {{16 - 8} \over 2} = 4\) ( thỏa mãn \(x > - 4\) ). +) \(m < 0\) hoặc \(m > 16\) thì (1) có hai nghiệm phân biệt \({x_1},{x_2}({x_1} < {x_2})\) . Ta có : \({x_1} < - 4 < {x_2} \Leftrightarrow ({x_1} + 4)({x_2} + 4) < 0 \) \(\Leftrightarrow {x_1}{x_2} + 4({x_1} + {x_2}) + 16 < 0\) . Theo hệ thức . Vi-et ta có \({x_1}{x_2} = 16\) và \({x_1} + {x_2} = m - 8\). Dẫn theo \(16 + 4(m - 8) + 16 < 0 \Leftrightarrow m < 0\) . Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 7. Phương trình mũ và lôgarit
|

 Tải ngay
Tải ngay