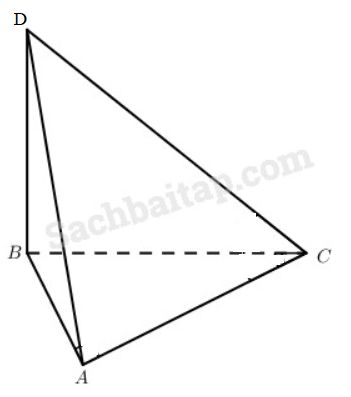
Câu 31 trang 120 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 31 trang 120 Sách bài tập Hình học 11 Nâng cao Chứng minh rằng nếu các cặp cạnh đối diện của tứ diện ABCD vuông góc với nhau từng đôi một thì trong bốn mặt của tứ diện có ít nhất một mặt là tam giác nhọn (cả ba góc của nó đều nhọn). Trả lời
Giả sử ABCD là tứ diện có tính chất \(AB \bot C{\rm{D}},AC \bot B{\rm{D}},A{\rm{D}} \bot BC\). Ta có: \(A{B^2} + C{{\rm{D}}^2} = A{C^2} + B{{\rm{D}}^2} = B{C^2} + A{{\rm{D}}^2}\). Từ đó, ta có \(\eqalign{ & A{B^2} + A{C^2} - B{C^2} \cr & = A{C^2} + A{{\rm{D}}^2} - C{{\rm{D}}^2} \cr & = A{{\rm{D}}^2} + A{B^2} - B{{\rm{D}}^2} \cr} \) Hệ thức này khẳng định các góc \(\widehat {BAC},\widehat {CA{\rm{D}}},\widehat {DAB}\) hoặc cùng nhọn, cùng vuông hoặc cùng tù. Tương tự như trên, ta chứng minh được góc tại bất cứ đỉnh nào của tứ diện ABCD cũng có tính chất đó. Do tính chất tổng các góc trong của một tam giác bằng 1800 nên tồn tại nhiều nhất một đỉnh của tứ diện mà tại đó ba góc cùng vuông hay cùng tù. Khi ấy mặt đối diện với đỉnh đó của tứ diện ABCD có cả ba góc đều nhọn. Vậy nên \(AB \bot C{\rm{D}},AC \bot B{\rm{D}}\) và \(A{\rm{D}} \bot BC\) thì trong bốn mặt của tứ diện ABCD có ít nhất một mặt là tam giác nhọn (cả ba góc của nó nhỏ hơn 90°). Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
-
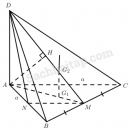
Câu 32 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 32 trang 120 Sách bài tập Hình học 11 Nâng cao
-
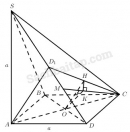
Câu 33 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 33 trang 120 Sách bài tập Hình học 11 Nâng cao
-
Câu 34 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 34 trang 120 Sách bài tập Hình học 11 Nâng cao
-
Câu 35 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 35 trang 120 Sách bài tập Hình học 11 Nâng cao

 Tải ngay
Tải ngay