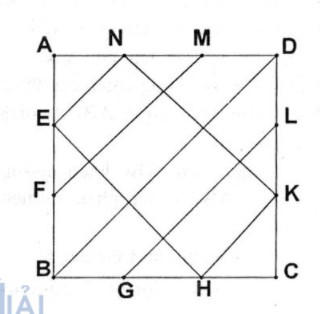
Câu 31 trang 160 Sách bài tập (SBT) Toán 8 tập 1Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm. Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm. Giải:
Diện tích hình vuông ABCD bằng \({1 \over 2}\).4.4 = 8 (\(c{m^2}\)) Diện tích tam giác DKN bằng \({1 \over 2}\).4.4 = 8(\(c{m^2}\)) Diện tích phần còn lại là : 36 – ( 8 + 8) = 20 (\(c{m^2}\)) Trong tam giác vuông AEN ta có: \(E{N^2} = A{N^2} + A{E^2}\)= 4 + 4 = 8 EN = \(2\sqrt 2 \) (cm) Trong tam giác vuông BHE ta có: \(E{H^2} = B{E^2} + B{H^2}\)= 16 + 16 = 32 EH = \(4\sqrt 2 \) (cm) Diện tích hình chữ nhật ENKH bằng \(2\sqrt 2 \). \(4\sqrt 2 \) =16 (\(c{m^2}\)) Nối đường chéo BD. Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 \(c{m^2}\) \({S_{AEPSN}} = {S_{AEN}} + {S_{EPSN}} = 2 + {{16} \over 4} = 6\) ((\(c{m^2}\))
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Diện tích tam giác
|
-
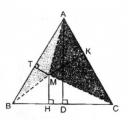
Câu 3.2 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
-
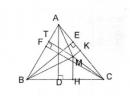
Câu 3.3 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
-
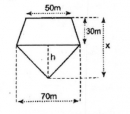
Câu 32 trang 161 Sách bài tập (SBT) Toán 8 tập 1-
Tính x, biết đa giác ở hình 188 có diện tích là 3375 m2.

 Tải ngay
Tải ngay