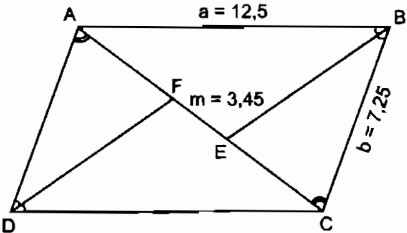
Câu 3.2 trang 89 Sách bài tập (SBT) Toán 8 tập 2Hãy tính độ dài đường chéo AC, biết EF = m = 3,45cm. Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F. Hãy tính độ dài đường chéo AC, biết EF = m = 3,45cm. (Tính chính xác đến hai chữ số thập phân) Giải: Vì ABCD là hình bình hành nên\(\widehat {ABC} = \widehat {ADC}\). Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra \(\widehat {ADF} = \widehat {CBE}\) Mặt khác, ta có: AD = CB = b; \(\widehat {DAF} = \widehat {BCE}\) (so le trong) Suy ra: ∆ ADF = ∆ CBE (g.c.g) ⇒ AF = CE Đặt AF = CE = x Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: \(\eqalign{ & {{AB} \over {BC}} = {{AE} \over {CE}} = {{AF + FE} \over {CE}} \cr & \Rightarrow {a \over b} = {{x + m} \over x} \Rightarrow x = {{mb} \over {a - b}} \cr & AC = 2x + m = {{2mb} \over {a - b}} + m = {{m\left( {a + b} \right)} \over {a - b}} \cr} \) Thay số, tính trên máy tính điện tử cầm tay ta được: \(AC = {{3,45\left( {12,5 + 7,25} \right)} \over {12,5 - 7,25}} \approx 12,98\) (cm) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Tính chất đường phân giác của tam giác
|
-

Câu 25 trang 89 Sách bài tập (SBT) Toán 8 tập 2
Cho hai tam giác A’B’C’ và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số chu vi của gai tam giác cũng bằng k.
-

Câu 27 trang 90 Sách bài tập (SBT) Toán 8 tập 2
Tính độ dài các cạnh của tam giác A’B’C’, biết rằng tam giác A’B’C’ đồng dạng với tam giác ABC
-
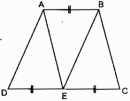
Câu 28 trang 90 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng ba tam giác ADE, ABE và BEC đông dạng với nhau từng đôi một.

 Tải ngay
Tải ngay