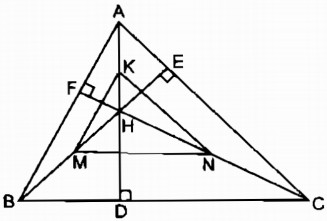
Câu 32 trang 91 Sách bài tập (SBT) Toán 8 tập 2Chứng minh rằng tam giác KMN đồng dạng với tam giác ABC với tỉ số đồng dạng k Tam giác ABC có ba góc nhọn và có trực tâm là điểm H. Gọi K, M, N thứ tự là trung điểm của các đoạn thẳng AH, BH, CH. Chứng minh rằng tam giác KMN đồng dạng với tam giác ABC với tỉ số đồng dạng k = \({1 \over 2}\) . Giải:
Trong tam giác AHB, ta có: K là trung điểm của AH (gt) M là trung điểm của BH (gt) Suy ra KM là đường trung bình của tam giác AHB. Suy ra: KM \( = {1 \over 2}AB\) (tính chất đường trung bình của tam giác ) Suy ra: \({{KM} \over {AB}} = {1 \over 2}\) (1) Trong tam giác AHC, ta có: K là trung điểm của AH (gt) N là trung điểm của CH (gt) Suy ra KN là đường trung bình của tam giác AHC. Suy ra: KN \( = {1 \over 2}AC\) (tính chất đường trung bình của tam giác ) Suy ra: \({{KN} \over {AC}} = {1 \over 2}\) (2) Trong tam giác BHC, ta có: M trung điểm của BH (gt) N trung điểm của CH (gt) Suy ra MN là đường trung bình của tam giác BHC. Suy ra: MN \( = {1 \over 2}BC\) (tính chất đường trung bình của tam giác ) Suy ra: \({{MN} \over {BC}} = {1 \over 2}\) (3) Từ (1), (2) và (3) suy ra: \({{KM} \over {AB}} = {{KN} \over {AC}} = {{MN} \over {BC}} = {1 \over 2}\) Vậy ∆ KMN đồng dạng ∆ ABC (c.c.c) Ta có hệ số tỉ lệ: k \( = {{KM} \over {AB}} = {1 \over 2}\). Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
|
-
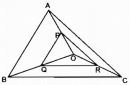
Câu 33 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
-
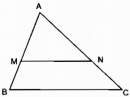
Câu 34 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k
-

Câu 5.1 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ? hãy đánh dấu gạch chéo vào ô trả lời thích hợp ở bảng sau:
-
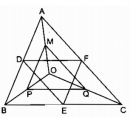
Câu 5.2 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó. Ba điểm D, E, F theo thứ tự là trung điểm các cạnh AB, BC và CA. Ba điểm M, P, Q theo thứ tự là trung điểm của các đoạn thẳng OA, OB và OC.

 Tải ngay
Tải ngay