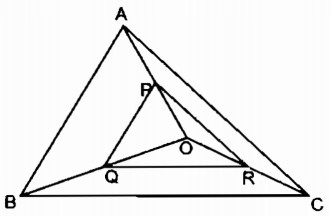
Câu 33 trang 91 Sách bài tập (SBT) Toán 8 tập 2Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC. Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. a. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC. b. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543cm. Giải:
a. Trong tam giác AOB, ta có: P là trung điểm của OA (gt) Q là trung điểm của OB (gt) Suy ra: PQ là đường trung bình của ∆ OAB. Suy ra: \(PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác ) Suy ra: \({{PQ} \over {AB}} = {1 \over 2}\) (1) Trong tam giác OAC, ta có: P là trung điểm của OA (gt) R là trung điểm của OC (gt) Suy ra: PR là đường trung bình của tam giác OAC. Suy ra: \(PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác ) Suy ra: \({{PR} \over {AC}} = {1 \over 2}\) (2) Trong tam giác OBC, ta có: Q là trung điểm của OB (gt) R là trung điểm của OC (gt) Suy ra: QR là đường trung bình của tam giác OBC. Suy ra: \(QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác ) Suy ra: \({{QR} \over {BC}} = {1 \over 2}\) (3) Từ (1), (2) và (3) suy ra: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {1 \over 2}\) Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c) b. Gọi p’ là chu vi tam giác PQR. Ta có: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {{PQ + PR + QR} \over {AB + AC + BC}} = {{p'} \over p}\) Vậy: \({{p'} \over p} = {1 \over 2} \Rightarrow p' = {1 \over 2}p = {1 \over 2}.543 = 271,5\) (cm) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
|
-
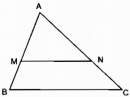
Câu 34 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k
-

Câu 5.1 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ? hãy đánh dấu gạch chéo vào ô trả lời thích hợp ở bảng sau:
-
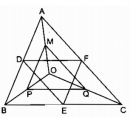
Câu 5.2 trang 91 Sách bài tập (SBT) Toán 8 tập 2
Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó. Ba điểm D, E, F theo thứ tự là trung điểm các cạnh AB, BC và CA. Ba điểm M, P, Q theo thứ tự là trung điểm của các đoạn thẳng OA, OB và OC.

 Tải ngay
Tải ngay