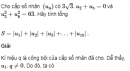Câu 3.58 trang 94 sách bài tập Đại số và Giải tích 11 Nâng caoCho cấp số nhân Cho cấp số nhân \(({u_n})\) với công bội \(q \in \left( {0;1} \right).\) Hãy tính tổng 25 số hạng đầu tiên của cấp số nhân đó, biết rằng \({u_1} + {u_3} = 3\) và \(u_1^2 + u_3^2 = 5\). Giải Ta có \(\left\{ \matrix{ Từ (1) suy ra \(u_1>0\). Do đó: \((I) \Leftrightarrow\left\{ \matrix{ \(\Leftrightarrow \left\{ \matrix{ \(\Leftrightarrow \left\{ \matrix{ Từ đó, kí hiệu S là tổng cần tính, ta được \(S = 2 \times {{1 - {{\left( {{1 \over {\sqrt 2 }}} \right)}^{25}}} \over {1 - \left( {{1 \over {\sqrt 2 }}} \right)}} = {{8191 + 4095.\sqrt 2 } \over {2048}}\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4. Cấp số nhân
|
-
Câu 3.61 trang 94 sách bài tập Đại số và Giải tích 11 Nâng cao
Ba số x , y , z , theo thứ tự đó lập thành một cấp số nhân
-
Câu 3.62 trang 94 sách bài tập Đại số và Giải tích 11 Nâng cao
Ba số x , y , z , theo thứ tự đó lập thành một cấp số nhân; đồng thời, chúng lần lượt là số hạng đầu, số hạng thứ ba và số hạng thứ chín của một cấp số cộng.

 Tải ngay
Tải ngay