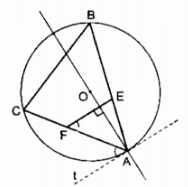
Câu 4.1, 4.2 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2Chứng minh góc BCF + góc BEF = 180. Câu 4.1 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2 Cho đường tròn tâm O bán kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O). Điểm E bất kỳ thuôc đoạn thẳng AB (và không trùng với A, B). Đường thẳng d đi qua điểm E và vuông góc với đường thẳng OA cắt đoạn thẳng AC tại điểm F. Chứng minh \(\widehat {BCF} + \widehat {BEF} = {180^0}\). Giải
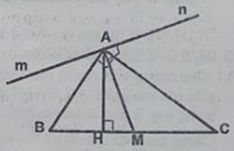
Kẻ tiếp tuyến At của đường tròn (O) At \( \bot OA\) (tính chất tiếp tuyến) \(EF \bot OA\) (gt) Suy ra: At // EF \(\widehat {EFA} = \widehat {CAt}\) (so le trong) \(\widehat {CBA} = \widehat {CAt}\) (hệ quả góc giữa tia tiếp tuyến và dây cung) Suy ra: \(\widehat {EFA} = \widehat {CBA}\) hay \(\widehat {EFA} = \widehat {CBE}\) \(\widehat {EFA} + \widehat {EFC} = {180^0}\) (hai góc kề bù) \(\overparen{CBE}\) + \(\overparen{EFC}\) = 1800 (1) Trong tứ giác BCFE ta có: \(\overparen{BCF}\) + \(\overparen{BEF}\) + \(\overparen{CBE}\) + \(\overparen{CFE}\) = 3600 (tổng các góc trong tứ giác) (2) Từ (1) và (2) suy ra: \(\widehat {BCF} + \widehat {BEF} = {180^0}\) Câu 4.2 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2 Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của các góc tạo bở AH và hai tia Am, An của đường thẳng mn. Giải
∆ABCvuông tại A, có AM là đường trung tuyến ứng với cạnh huyền BC \( \Rightarrow AM = MB = MC = {1 \over 2}BC\) (tính chất tam giác vuông) \( \Rightarrow \) ∆AMB cân tại M \( \Rightarrow \widehat B = \widehat {BAM}\) (1) \(mn \bot AM\) (gt) \( \Rightarrow \widehat {mAM} + \widehat {BAM} = {90^0}\) (2) ∆AHB vuông tại H \( \Rightarrow \widehat B + \widehat {BAH} = {90^0}\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {mAB} = \widehat {BAH}\). Vậy AB là tia phân giác của \(\widehat {mAH}\). ∆AMC cân tại M \( \Rightarrow \widehat {MAC} = \widehat C\) (4) \(mn \bot AM\) (gt) \( \Rightarrow \widehat {MAC} + \widehat {nAC} = {90^0}\) (5) ∆AHC vuông tại H \( \Rightarrow \widehat {HAC} + \widehat C = {90^0}\) (6) Từ (4), (5) và (6) suy ra: \(\widehat {HAC} = \widehat {nAC}\). Vậy AC là tia phân giác của \(\widehat {HAn}\) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
|
-
Câu 26 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2
Ngồi trên một đỉnh núi cao 1km thì có thể nhìn thấy một địa điểm T trên mặt đất với khoảng cách tối đa là bao nhiêu.
-
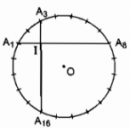
Câu 28 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2
Chứng minh rằng dây A1A8 vuông góc với dây A3A16.

 Tải ngay
Tải ngay