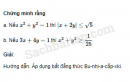Tải ngay
Câu 4.19 trang 105 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.19 trang 105 SBT Đại số 10 Nâng cao. Chứng minh rằng : Nếu \(0 < a < b\) thì \(a < \dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}} < \sqrt {{\rm{a}}b} < \dfrac{{a + b}}{2} < b.\) Giải: Do \(0 < a < b\) nên \(\dfrac{a}{b} < 1\) suy ra \(a\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) = 1 + \dfrac{a}{b} < 2\) tức là \(a < \dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}}.\) (1) Lại có \(\dfrac{1}{a} + \dfrac{1}{b} > 2\sqrt {\dfrac{1}{{ab}}} \) nên \(\dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}} < \sqrt {{\rm{a}}b} .\) (2) Do \(0 < a < b\) nên \(\sqrt {{\rm{a}}b} < \dfrac{{a + b}}{2} < b.\) (3) Từ (1), (2) và (3) suy ra điều cần chứng minh. Sachbaitap.com
Xem thêm tại đây:
Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
|
