Câu 4.21 trang 207 sách bài tập (SBT) - Giải tích 12a) Cho số phức z. Chứng minh rằng z là số thực khi và chỉ khi: a) Cho số phức z. Chứng minh rằng z là số thực khi và chỉ khi \(z = \bar z\) b) Chứng tỏ rằng số phức sau là một số thực: \(z = - {{3 + 2i\sqrt 3 } \over {\sqrt 2 + 3i}} + {{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}}\) Hướng dẫn làm bài a) Hiển nhiên \(z \in R\) thì \(z = \bar z\) . Ngược lại, giả sử z = a + bi và \(z = \bar z\). Từ đó suy ra a + bi = a – bi và do đó b = - b hay b = 0. Vậy \(z \in R\) b) Ta có \(z = {{ - 3 - 2i\sqrt 3 } \over {\sqrt 2 + 3i}} + {{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}}\), suy ra \(\bar z = \overline {({{ - 3 - 2i\sqrt 3 } \over {\sqrt 2 + 3i}} + {{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}})} = \overline {({{ - 3 - 2i\sqrt 3 } \over {\sqrt 2 + 3i}})} + \overline {({{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}})} \)\( = \overline {{{ - 3 - 2i\sqrt 3 } \over {\sqrt 2 + 3i}}} + \overline {{{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}}} = {{ - 3 + 2i\sqrt 3 } \over {\sqrt 2 - 3i}} + {{ - 3 - 2i\sqrt 3 } \over {\sqrt 2 + 3i}} = z\) Vậy \(z \in R\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Phép chia số phức
|
-
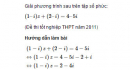
Câu 4.23 trang 208 sách bài tập (SBT) - Giải tích 12
Giải phương trình sau trên tập số phức : (1 – i)z + (2 – i) = 4 – 5i
-
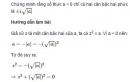
Câu 4.25 trang 209 sách bài tập (SBT) - Giải tích 12
Chứng minh rằng số thực a < 0 chỉ có hai căn bậc hai phức là

 Tải ngay
Tải ngay









