Tải ngay
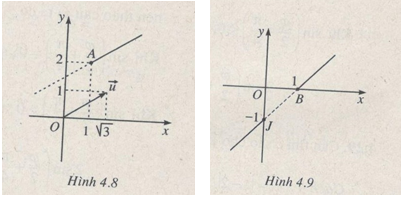
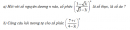Câu 4.26 trang 181 sách bài tập Giải tích 12 Nâng caoXác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau: a) Một acgumen của \(z - \left( {1 + 2i} \right)\) bằng \({\pi \over 6}\) b) Một acgumen của \(z + i\) bằng một acgumen của \(z - 1\) Giải a) Tia có gốc A (là điểm biểu diễn số \(1 + 2i\)) với vectơ chỉ hướng \(\overrightarrow u \) biểu diễn số \(\sqrt 3 + i\) (tức là \(\overrightarrow u \) có một acgumen là \({\pi \over 6}\)) (không kể điểm A) (h.4.8) b) Các điểm B, J theo thứ tự biểu diễn số 1, -i thì tập hợp cần tìm là các điểm thuộc đường thẳng BJ nằm ngoài đoạn BJ (h.4.9) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Dạng lượng giác của số phức. Ứng dụng
|
-
Câu 4.30 trang 182 sách bài tập Giải tích 12 Nâng cao
Ác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z sao cho
