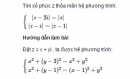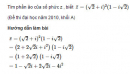Câu 4.38 trang 211 sách bài tập (SBT) - Giải tích 12Tìm số phức z, biết: Tìm số phức z, biết: a) \(\bar z = {z^3}\) b) \(|z| + z = 3 + 4i\) Hướng dẫn làm bài a) Ta có \(z\bar z = |z{|^2}\) nên từ \(\bar z = {z^3} \Rightarrow |z{|^2} = {z^4}\) Đặt z = a+ bi , suy ra: \({a^4} + {b^4} - 6{a^2}{b^2} + 4ab({a^2} - {b^2})i = {a^2} + {b^2}\) (*) Do đó, ta có: \(4ab({a^2} - {b^2}) = 0\) (**) Từ (**) suy ra các trường hợp sau: +) a = b = 0 ⟹ z = 0 +) \(a = 0,b \ne 0\) : Thay vào (*), ta có \({b^4} = {b^2} \Rightarrow b = \pm 1 \Rightarrow z = \pm i\) +) \(b = 0,a \ne 0\) : Tương tự, ta có \(a = \pm 1 \Rightarrow z = \pm 1 \) +) \(a \ne 0,b \ne 0 \Rightarrow {a^2} - {b^2} = 0 \Rightarrow {a^2} = {b^2}\) , thay vào (*) , ta có: 2a2(2a2 + 1) = 0, không có a nào thỏa mãn (vì \(a \ne 0\) ) b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra \(\sqrt {{a^2} + {b^2}} + a + bi = 3 + 4i \Rightarrow b = 4\) và \(\sqrt {{a^2} + 16} + a = 3\) \( \Rightarrow {a^2} + 16 = {(3 - a)^2} = 9 - 6a + {a^2}\) \(\Rightarrow 6a = - 7 \Rightarrow a = - {7 \over 6}\) Vậy \(z = - {7 \over 6} + 4i\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Ôn tập Chương IV - Số phức
|
-
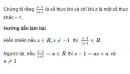
Câu 4.40 trang 211 sách bài tập (SBT) - Giải tích 12
Chứng tỏ rằng phân số đã cho là số thực khi và chỉ khi z là một số thực khác – 1.
-
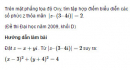
Câu 4.42 trang 211 sách bài tập (SBT) - Giải tích 12
Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn | z – (3 – 4i)| = 2.

 Tải ngay
Tải ngay