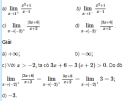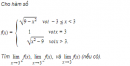Câu 4.44 trang 141 sách bài tập Đại số và Giải tích 11 Nâng caoTìm các giới hạn sau Tìm các giới hạn sau a) \(\mathop {\lim }\limits_{x \to 3} {\left( {3 - 4x} \right)^2}\) b) \(\mathop {\lim }\limits_{x \to - 1} {{{x^2} + x + 1} \over {2{x^5} + 3}}\) c) \(\mathop {\lim }\limits_{x \to 1} {{{x^2}\left( {2x - 1} \right)} \over {{x^4} + x + 1}}\) d) \(\mathop {\lim }\limits_{x \to 2} \root 3 \of {{{{x^2} - x + 1} \over {{x^2} + 2x}}} \) e) \(\mathop {\lim }\limits_{x \to 3} \sqrt {{{9{x^2} - x} \over {\left( {2x - 1} \right)\left( {{x^4} - 3} \right)}}} \) f) \(\mathop {\lim }\limits_{x \to 0} {{1 - {1 \over x}} \over {1 + {1 \over x}}}\) g) \(\mathop {\lim }\limits_{x \to + \infty } \left| {{{ - {x^2} - x + 6} \over {{x^2} + 3x}}} \right|\) h) \(\mathop {\lim }\limits_{x \to - 2} {{{{\left( {{x^2} - x + 6} \right)}^2}} \over {{x^3} + 2{x^2}}}\) Giải a) 81; b) 1; c) \({1 \over 3};\) d) \({{\root 3 \of 3 } \over 2};\) e) \({{\sqrt 5 } \over 5};\) f) Với mọi \(x \ne 0,\) ta có \({{1 - {1 \over x}} \over {1 + {1 \over x}}} = {{x - 1} \over {x + 1}}\) Do đó \(\mathop {\lim }\limits_{x \to 0} {{1 - {1 \over x}} \over {1 + {1 \over x}}} = \mathop {\lim }\limits_{x \to 0} {{x - 1} \over {x + 1}} = - 1;\) g) \({{ - {x^2} - x + 6} \over {{x^2} + 3x}} = {{2 - x} \over x}\) với mọi \(x \ne -3\) \(\mathop {\lim }\limits_{x \to - 3} {{ - {x^2} - x + 6} \over {{x^2} + 3x}} = \mathop {\lim }\limits_{x \to - 3} {{2 - x} \over x} = -{5 \over 3}.\) Do đó \(\mathop {\lim }\limits_{x \to - 3} \left| {{{ - {x^2} - x + 6} \over {{x^2} + 3x}}} \right| = \left| { - {5 \over 3}} \right| = {5 \over 3}.\) h) \({{{{\left( {{x^2} - x - 6} \right)}^2}} \over {{x^3} + 2{x^2}}} = {{{{\left( {x - 3} \right)}^2}\left( {x + 2} \right)} \over {{x^2}}}\) với mọi \(x \ne 2\) \(\mathop {\lim }\limits_{x \to - 2} {{{{\left( {{x^2} - x - 6} \right)}^2}} \over {{x^3} + 2{x^2}}} = 0\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4: Định nghĩa và một số định lí về giới hạn của hàm số
|

 Tải ngay
Tải ngay