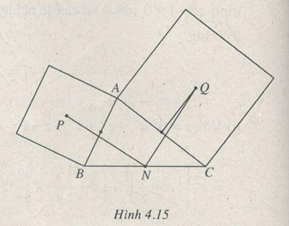
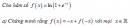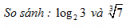Câu 4.56 trang 184 sách bài tập Giải tích 12 Nâng cao

a) Trong  mặt phẳng phức cho điểm A biểu diễn số phức \(\omega \). Chứng minh rằng phép biến đổi của mặt phẳng phức biến điểm biểu diễn số phức z tùy ý thành biểu diễn số phức z’ sao cho \(z' - \omega  = i\left( {z - \omega } \right)\) là phép quay tâm A góc quay \({\pi  \over 2}\)

b) Giả sử ba đỉnh A, B, C của tam giác ABC trong mặt phẳng phức theo thứ tự biểu diễn các số \(\alpha ,\beta ,\gamma \). Gọi P, Q theo thứ tự là tâm các hình vuông dựng bên ngoài ABC trên các cạnh AB, AC và gọi N là trung điểm của BC. Tìm các số phức biểu diễn bởi các vectơ \(\overrightarrow {NQ} ,\overrightarrow {NP} \) rồi chứng minh NQP là tam giác vuông cân.

Giải

a) M là điểm biểu diễn số phức z, M’ là điểm biểu diễn số phức z’.

Khi M trùng với A tức là \(z = \omega \) thì \(z' = \omega \) nên A biến thành chính nó. Khi M không trung với A thì \(\left| {\overrightarrow {AM'} } \right| = \left| {z' - \omega } \right| = \left| i \right|\left| {z - \omega } \right| = \left| {z - \omega } \right| = \left| {\overrightarrow {AM} } \right|\) và một acgumen của \({{z' - \omega } \over {z - \omega }} = i\) là số đo góc lượng giác (AM,AM') nên góc này là \({\pi  \over 2}\). Từ đó phép biến đổi đang xét là phép quay tâm A, góc quay  \({\pi  \over 2}\)

b) (h.4.15) Giả sử ta đi dọc chu vi tam giác ABC theo ngược chiều quay kim đồng hồ. Khi đó Q là ảnh của C qua phép quay tâm là trung điểm của CA góc quay \({\pi  \over 2}\) nên nếu kí hiệu q là số phức biểu diễn bởi điểm Q thì theo câu a) ta có

\(q - {{\gamma  + \alpha } \over 2} = i\left( {\gamma  - {{\gamma  + \alpha } \over 2}} \right)\)

Từ đó

\(q = {1 \over 2}\left[ {\left( {1 + i} \right)\gamma  + \left( {1 - i} \right)\alpha } \right]\)

Đổi \(\alpha \) thành \(\beta \), \(\gamma \) thành \(\alpha \), ta suy ra p biểu diễn bởi P là

\(p = {1 \over 2}\left[ {\left( {1 + i} \right)\alpha  + \left( {1 - i} \right)\beta } \right]\)

Vậy \(\overrightarrow {NP} \) biểu diễn số phức \(p - {1 \over 2}\left( {\beta  + \gamma } \right) = {1 \over 2}\left[ {\left( {1 + i} \right)\alpha  - i\beta  - \gamma } \right]\) và \(\overrightarrow {NQ} \) biểu diễn số phức

\(q - {1 \over 2}\left( {\beta  + \gamma } \right) = {1 \over 2}\left[ {\left( {1 - i} \right)\alpha  - \beta  + i\gamma } \right]\). Rõ  ràng \(i,{1 \over 2}\left[ {\left( {1 - i} \right)\alpha  - \beta  + i\gamma } \right] = {1 \over 2}\left[ {\left( {1 + i} \right)\alpha  - i\beta  - \gamma } \right]\), nên suy ra \(NQ = NP\) và \(\overrightarrow {NQ},\overrightarrow {NP}  \) vuông góc (h.4.15)

Sachbaitap.com