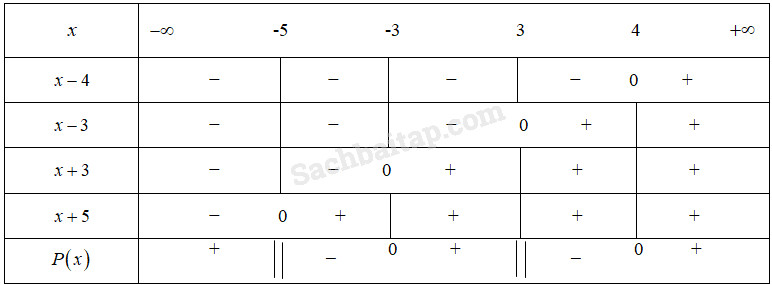
Câu 4.65 trang 113 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.65 trang 113 SBT Đại số 10 Nâng cao Tìm tập xác định của hàm số sau: \(f\left( { {x}} \right) = \sqrt {\dfrac{{3 - 3{ {x}}}}{{ - {x^2} - 2{ {x}} + 15}} - 1} .\) Giải: Tập xác định của hàm số \(y = f(x)\) gồm các giá trị thỏa mãn \(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{\dfrac{{3 - 3{ {x}}}}{{ - {x^2} - 2{ {x}} + 15}} - 1 \ge 0}\\{ - {x^2} - 2{ {x}} + 15 \ne 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{3 - 3{ {x}} - 15 + 2{ {x}} + {{ {x}}^2}}}{{ - \left( {{{ {x}}^2} + 2{ {x}} - 15} \right)}} \ge 0}\\{{x^2} - 2{ {x}} + 15 \ne 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{{{ {x}}^2} - x - 12}}{{{x^2} + 2{ {x}} - 15}} \le 0}\\{{x^2} + 2{ {x}} - 15 \ne 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{\left( {{ {x}} + 3} \right)\left( {{ {x}} - 4} \right)}}{{\left( {{ {x}} - 3} \right)\left( {{ {x}} + 5} \right)}} \le 0}\\{{x^2} + 2{ {x}} - 15 \ne 0.}\end{array}} \right.\end{array}\) Đặt \(P\left( { {x}} \right) = \dfrac{{\left( {{ {x}} + 3} \right)\left( {{ {x}} - 4} \right)}}{{\left( {{ {x}} - 3} \right)\left( {{ {x}} + 5} \right)}}\) Lập bảng xét dấu \(P(x)\) :
Từ bảng xét dấu suy ra tập xác định của hàm số \(f(x)\) là : \(\left( { - 5; - 3} \right] \cup \left( {3;4} \right].\) Sachbaitap.com
Xem thêm tại đây:
Bài 7. Bất phương trình bậc hai
|

 Tải ngay
Tải ngay