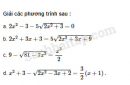Câu 4.69 trang 114 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.69 trang 114 SBT Đại số 10 Nâng cao Tìm các giá trị của m để phương trình : a. \({x^2} + 2\left( {m + 1} \right)x + 9m - 5 = 0\) có hai nghiệm âm phân biệt ; b. \(\left( {m - 2} \right){x^2} - 2m{ {x}} + m + 3 = 0\) có hai nghiệm dương phân biệt. Giải: a. Phương trình có hai nghiệm âm phân biệt khi và chỉ khi: \(\eqalign{& \left\{ \matrix{\Delta ' = {\left( {m + 1} \right)^2} - \left( {9m - 5} \right) > 0 \hfill \cr {S \over 2} = - \left( {m + 1} \right) < 0 \hfill \cr ac = 9m - 5 > 0 \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{{m^2} - 7m + 6 > 0 \hfill \cr m > - 1 \hfill \cr m > {5 \over 9} \hfill \cr} \right. \cr & \Leftrightarrow \left\{ \matrix{m > - 1 \hfill \cr m > {5 \over 9} \hfill \cr m > 6\,\,\,hoặc\,\,\,m < 1 \hfill \cr} \right. \cr} \) \(\Leftrightarrow m > 6\) hoặc \({5 \over 9} < m < 1\) Vậy các giá trị cần tìm của m là \(m \in \left( {\dfrac{5}{9};1} \right) \cup \left( {6; + \infty } \right).\) b. \(m \in \left( { - \infty ; - 3} \right) \cup \left( {2;6} \right).\) Sachbaitap.com
Xem thêm tại đây:
Bài 7. Bất phương trình bậc hai
|

 Tải ngay
Tải ngay