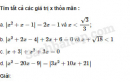Câu 4.73 trang 115 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.73 trang 115 SBT Đại số 10 Nâng cao Giải các phương trình sau : a. \(2{{ {x}}^2} - 3 - 5\sqrt {2{{ {x}}^2} + 3} = 0\) b. \(2{{ {x}}^2} + 3{ {x}} + 3 = 5\sqrt {2{{ {x}}^2} + 3{ {x}} + 9} \) c. \(9 - \sqrt {81 - 7{{ {x}}^3}} = \dfrac{{{{ {x}}^3}}}{2}\) d. \({x^2} + 3 - \sqrt {2{{ {x}}^2} - 3{ {x}} + 2} = \dfrac{3}{2}\left( {{ {x}} + 1} \right).\) Giải: a. \({x_1} = \sqrt {\dfrac{{33}}{2}} ,{x_2} = - \sqrt {\dfrac{{33}}{2}} .\). Hướng dẫn. Phương trình được biến đổi thành \(2{{ {x}}^2} + 3 - 5\sqrt {2{{ {x}}^2} + 3} - 6 = 0\) (*) Đặt \(t = \sqrt {2{{ {x}}^2} + 3} \ge 0.\) Khi đó (*) trở thành \({t^2} - 5t - 6 = 0\) và có hai nghiệm \({t_1} = - 1,{t_2} = 6.\) Do \(t ≥ 0\), nên chỉ lấy \(t = 6\). b. \(x = 3;x = - \dfrac{9}{2}.\) Hướng dẫn. Đặt \(t = \sqrt {2{{ {x}}^2} + 3{ {x}} + 9} .\) c. \(x = 0 ; x = 2\). Hướng dẫn. Đặt \(t = \sqrt {81 - 7{{ {x}}^3}} \) d. \(x = 1;x = \dfrac{1}{2}.\) Hướng dẫn. Đặt \(t = \sqrt {2{{ {x}}^2} - 3{ {x}} + 2} .\) Sachbaitap.com
Xem thêm tại đây:
Bài 8. Một số phương trình và bất phương trình quy về bậc hai
|

 Tải ngay
Tải ngay