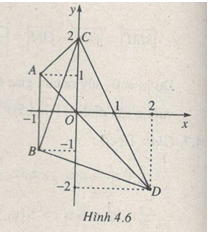
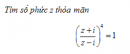Câu 4.9 trang 178 sách bài tập Giải tích 12 Nâng cao

Cho A, B, C, D là bốn điểm trong mặt phẳng phức biểu diễn theo thứ tự các số:

\( - 1 + i\),            \( - 1 - i\),              \(2i,\),               \(2 - 2i\),

Tìm các số  \({z_1},{z_2},{z_3},{z_4}\) theo thứ tự biểu diện bởi các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {BC} ,\overrightarrow {BD} \). Tính \({{{z_1}} \over {{z_2}}},{{{z_3}} \over {{z_4}}}\) và từ đó suy ra A, B, C, D cùng nằm trên một đường tròn (Xem bài tập 4.8). Tâm đường tròn đó biểu diễn số phức nào ?

Giải

(h.4.6)

\(\overrightarrow {AC} \) biểu diễn số phức \({z_1} = 1 + i,(\overrightarrow {AD} \) biểu diễn số phức \({z_2} = 3 - 3i,\)do \({{{z_1}} \over {{z_2}}} = {{1 + i} \over {3 - 3i}} = {i \over 3}\) nên \(\overrightarrow {AC} .\overrightarrow {AD}  = 0\) (xem bài tập 4.8)

\(\overrightarrow {BC} \) biểu diễn số phức \({z_3} = 1 + 3i,(\overrightarrow {BD} \) biểu diễn số phức \({z_4} = 3 - i.\)

Do \({{{z_3}} \over {{z_4}}} = {{1 + 3i} \over {3 - i}} = i\) nên \(\overrightarrow {BC} .\overrightarrow {BD}  = 0\) (xem bài tập 4.8)

Vậy CD là một đường kính của đường tròn đi qua bốn điểm A, B, C, D. Tâm đường tròn đó là trung điểm CD nên nó biểu diễn số \({{2i + \left( {2 - 2i} \right)} \over 2} = 1\)  

Sachbaitap.com