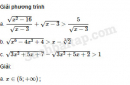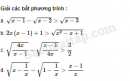Tải ngay
Câu 4.96 trang 118 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.96 trang 118 SBT Đại số 10 Nâng cao Xác định các giá trị của tham số m để mỗi bất phương trình sau nghiệm đúng với mọi x. a. \(\dfrac{{{x^2} + mx - 1}}{{2{x^2} - 2x + 3}} < 1\) b. \( - 4 < \dfrac{{2{x^2} + mx - 4}}{{ - {x^2} + x - 1}} < 6\) Giải: a. Do \(2{x^2} - 2x + 3 > 0\) với mọi x nên bất phương trình tương đương với : \({x^2} - \left( {2 + m} \right)x + 4 > 0.\) Để bất phương trình nghiệm đúng với mọi x, điều kiện cần và đủ là \(\Delta = {\left( {2 + m} \right)^2} - 16 < 0\) hay \( - 6 < m < 2.\) b. \(m \in \left( { - 2;4} \right).\) Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
|
