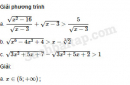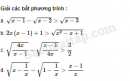Câu 4.97 trang 118 SBT Đại số 10 Nâng cao

Tùy theo giá trị của tham số m, hãy biện luận số nghiệm phương trình

\(\left( {m + 3} \right){x^4} - \left( {2m - 1} \right){x^2} - 3 = 0\)

Giải:

Đặt \(t = {x^2}\) phương trình trở thành \(f\left( t \right) = \left( {m + 3} \right){t^2} - \left( {2m - 1} \right)t - 3 = 0,t \ge 0.\)

● Nếu m + 3 = 0, tức là m = -3 thì \(f\left( t \right) = 7t - 3 = 0,\) từ đó \(t = \dfrac{3}{7}.\) Suy ra phương trình đã cho có hai nghiệm \(x =  \pm \sqrt {\dfrac{3}{7}} .\)

● Nếu \(m + 3 ≠ 0 ⇔ m ≠ -3.\)

Khi đó, \(\Delta  = {\left( {2m - 1} \right)^2} + 12\left( {m + 3} \right) = 4{m^2} + 8m + 37 > 0\) với mọi m nên phương trình f(t) = 0 luôn có hai nghiệm phân biệt khác 0 (vì \(c = -3 ≠ 0\)).

+) Phương trình \(f(t) = 0\) có hai nghiệm dương khi và chỉ khi :

\(\left\{ {\begin{array}{*{20}{c}}{S = \dfrac{{2m - 1}}{{m + 3}} > 0}\\{P = \dfrac{{ - 3}}{{m + 3}} > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2m - 1 < 0}\\{m + 3 < 0}\end{array}} \right. \Leftrightarrow m <  - 3.\)

Khi đó phương trình đã cho có bốn nghiệm phân biệt.

+) Phương trình \(f(t) = 0\) có hai nghiệm âm khi và chỉ khi:

\(\left\{ {\begin{array}{*{20}{c}}{S = \dfrac{{2m - 1}}{{m + 3}} < 0}\\{P = \dfrac{{ - 3}}{{m + 3}} > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2m - 1 > 0}\\{m + 3 < 0}\end{array}} \right.\)

\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m > \dfrac{1}{2}}\\{m <  - 3}\end{array}} \right.\) (không tồn tại m).

+) Phương trình \(f(t) = 0\) có một nghiệm âm và một nghiệm dương khi và chỉ khi

\(ac = (-3)(m + 3) < 0 ⇔ m > -3.\)

Khi đó phương trình đã cho có hai nghiệm phân biệt.

Tóm lại : Với \(m ≥ -3\) phương trình có hai nghiệm phân biệt.

Với \(m < -3\) phương trình có bốn nghiệm phân biệt.

Sachbaitap.com