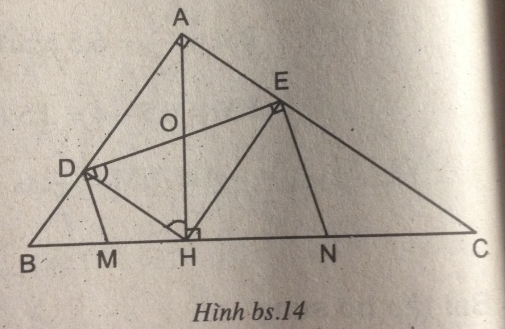
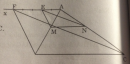
Câu 8.3 trang 96 Sách bài tập (SBT) Toán 8 tập 2

Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.

Gọi D và E là hình chiếu của H trên AB và AC.

a. Tính độ dài DE

b. Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.

c. Tính diện tích tứ giác DENM.

Giải:

a. Xét hai tam giác vuông ABH và CAH có:

\(\widehat {ABH} = \widehat {CAH}\) (cùng phụ với góc BAH)

Do đó ∆ ABH đồng dạng ∆ CAH (g.g).

Suy ra: \({{AH} \over {CH}} = {{BH} \over {AH}}\)

\(\eqalign{  &  \Rightarrow A{H^2} = BH.CH = 4.9  \cr  &  \Rightarrow AH = \sqrt {4.9}  = 6(cm) \cr} \)

Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.

Suy ra: DE = AH = 6 (cm)

b. Xét tam giác MDH có \(\widehat {MDH} = \widehat {MHD}\) (vì cùng bằng góc vuông trừ đi góc bằng nhau \(\widehat {ODH} = \widehat {OHD}\) )

Suy ra tam giác MDH cân tại M, do đó MD = MH.     (1)

Vì BHD là tam giác vuông tại D nên MD = BM.

Vậy M là trung điểm của BH

Tương tự, ta cũng có N là trung điểm của CH.

c. Theo chứng minh trên, ta có:

\(\eqalign{  & DM = MH = {1 \over 2}BH = {1 \over 2}.4 = 2(cm)  \cr  & EN = NH = {1 \over 2}CH = {1 \over 2}.9 = 4,5(cm)  \cr  & DE = AH = 6(cm) \cr} \)

DENM là hình thang vuông, do đó diện tích của nó là:

\({S_{DENM}} = {1 \over 2}\left( {DM + EN} \right)DE = {1 \over 2}.\left( {2 + 4,5} \right).6 = 19,5(c{m^2})\).

Sachbaitap.com