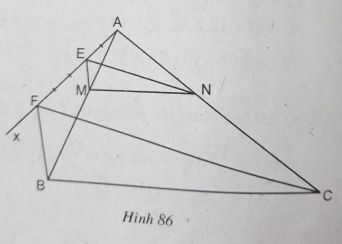
Câu 51 trang 97 Sách bài tập (SBT) Toán 8 tập 2Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không ? Vì sao ? Cho tam giác ABC. a. Tìm trên cạnh AB điểm M sao cho \({{AM} \over {MB}} = {2 \over 3}\); tìm trên cạnh AC điểm N sao cho \({{AN} \over {NC}} = {2 \over 3}\) b. Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không ? Vì sao ? c. Cho biết chu vi và diện tích tam giác ABC thứ tự là P và S. Tính chu vi và diện tích tam giác AMN. Giải:
a. Cách vẽ: - Kẻ tia Ax bất kì khác tia AB, AC. - Trên tia Ax, lấy hai điểm E và F sao cho AE = 2 (cm), EF = 3 (cm) - Kẻ đường thẳng FB. - Từ E kẻ đường thẳng song song với FB cắt AB tại M - Kẻ đường thẳng FC - Từ E kẻ đường thẳng song song với FC cắt AC tại N Ta có M, N là hai điểm cần vẽ. Chứng minh: Trong tam giác AFB, ta có: EM // FB Theo Định lí Ta-lét, ta có: \({{AM} \over {MB}} = {{AE} \over {EF}} = {2 \over 3}\) Trong tam giác AFC, ta có: EN // FC Theo Định lí Ta-lét, ta có: \({{AN} \over {NC}} = {{AE} \over {EF}} = {2 \over 3}\) Vậy M, N là hai điểm cần tìm. b. Trong tam giác ABC, ta có: \({{AM} \over {MB}} = {{AN} \over {NC}} = {2 \over 3}\) Suy ra: MN // BC (theo định lí đảo của định lí Ta-lét) c. Gọi p’ và S’ là chu vi và diện tích của ∆ AMN Trong tam giác ABC, ta có: MN // BC Suy ra: ∆ AMN đồng dạng ∆ ABC Theo tính chất hai tam giác đồng dạng ta có: \(\eqalign{ & {{p'} \over p} = {2 \over 5} = k \Rightarrow p' = {2 \over 5}p \cr & {{S'} \over S} = {\left( {{2 \over 5}} \right)^2} = {4 \over 25} = {k^2} \Rightarrow S' = {4 \over 25}S \cr} \) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương III - Tam giác đồng dạng
|
-
Câu 55 trang 98 Sách bài tập (SBT) Toán 8 tập 2
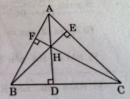
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH

 Tải ngay
Tải ngay