Tải ngay
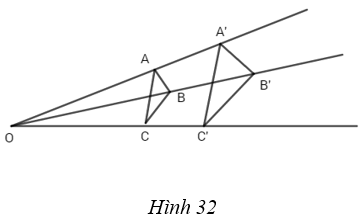
Câu 53 trang 14 Sách bài tập Hình Học 11 Nâng caoChứng minh rằng có phép vị tự biến tam giác này thành tam giác kia. 53. Trang 14 Sách bài tập Hình Học 11 Nâng cao Cho hai tam giác ABC và A’B’C’ không bằng nhau nhưng có các cạnh tương ứng song song: AB // A’B’, BC // B’C’ và CA // C’A’. Chứng minh rằng có phép vị tự biến tam giác này thành tam giác kia. Giải (h.32)
Vì AB và A’B’ song song nhưng không bằng nhau nên hai đường thẳng AA’ và BB’ cắt nhau tại điểm O. Gọi V là phép vị tự tâm O tỉ số \(k = {{OA'} \over {OA}}\) Thì V biến điểm C thành điểm C1 sao cho: \(A'{C_1}//AC;\,B'{C_1}\,//BC.\) Suy ra C1 trùng với C’, tức là V cũng biến C thành C’. Vậy ta có điều phải chứng minh. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 6, 7: Phép vị tự. Phép đồng dạng
|
-
Câu 54 trang 14 Sách bài tập Hình Học 11 Nâng cao
Cho hai phép vị tự V1 có tâm O1 tỉ số k1 và V2 có tâm O2 tỉ số k2. Gọi F là hợp thành của V1 và V2.
-
Câu 55 trang 14 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng mỗi bộ ba điểm sau đây thẳng hàng.
-
Câu 56 trang 14 Sách bài tập Hình Học 11 Nâng cao
Nếu thay giả thiết “tiếp xúc ngoài” bằng “tiếp xúc trong” thì kết quả trên sẽ thay đổi như thế nào?
-
Câu 57 trang 14 Sách bài tập Hình Học 11 Nâng cao
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B.
