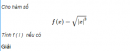Câu 5.3 trang 179 sách bài tập Đại số và Giải tích 11 Nâng caoCho hàm số f (x) = x3 (C) a) Tại những điểm nào của (C) thì tiếp tuyến của (C) có hệ số góc bằng 1. Cho hàm số f (x) = x3 (C) a) Tại những điểm nào của (C) thì tiếp tuyến của (C) có hệ số góc bằng 1. b) Liệu có tiếp tuyến nào của (C) mà tiếp tuyến đó có hệ số góc bằng âm? Giải a) \(\left( {{{\sqrt 3 } \over 3};{{\sqrt 3 } \over 9}} \right)\) và \(\left( {{{ - \sqrt 3 } \over 3};{{ - \sqrt 3 } \over 9}} \right)\) b) Muốn có tiếp tuyến của đồ thị hàm số \(y = {x^3}\) mà hệ số góc của tiếp tuyến đó âm thì phải tồn tại điểm \({x_0}\) sao cho \(f'\left( {{x_0}} \right) < 0.\) Ở đây \(f'\left( x \right) = 3{x^2} \ge 0\,\,\left( {\forall x \in R} \right)\); Vậy không có tiếp tuyến nào của đồ thị hàm số đã cho mà hệ số góc của nó âm. Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 1: Khái niệm đạo hàm
|
-

Câu 5.4 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
Cho parabol (C) có phương trình y = f (x) = kx2 (k là hằng số khác 0)
-
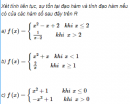
Câu 5.6 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
Xét tính liên tục, sự tồn tại đạo hàm và tính đạo hàm nếu có của các hàm số sau đây trên R
-
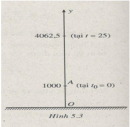
Câu 5.7 trang 179 sách bài tập Đại số và Giải tích 11 Nâng cao
Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với vận tốc ban đầu

 Tải ngay
Tải ngay