Câu 6.2 trang 32 Sách bài tập (SBT) Toán 8 tập 1Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện : Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện : a. \({1 \over {{x^2} + x + 1}} - Q = {1 \over {x - {x^2}}} + {{{x^2} + 2x} \over {{x^3} - 1}}\) b. \({{2x - 6} \over {{x^3} - 3{x^2} - x + 3}} + Q = {6 \over {x - 3}} - {{2{x^2}} \over {1 - {x^2}}}\) Giải: a. \({1 \over {{x^2} + x + 1}} - Q = {1 \over {x - {x^2}}} + {{{x^2} + 2x} \over {{x^3} - 1}}\) \(\eqalign{ & Q = {1 \over {{x^2} + x + 1}} - {1 \over {x - {x^2}}} - {{{x^2} + 2x} \over {{x^3} - 1}} \cr & Q = {1 \over {{x^2} + x + 1}} + {1 \over {x\left( {x - 1} \right)}} - {{{x^2} + 2x} \over {\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} \cr & Q = {{x\left( {x - 1} \right) + {x^2} + x + 1 - x\left( {{x^2} + 2x} \right)} \over {x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} \cr & Q = {{{x^2} - x + {x^2} + x + 1 - {x^3} - 2{x^2}} \over {x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = {{1 - {x^3}} \over {x\left( {{x^3} - 1} \right)}} = {{ - \left( {{x^3} - 1} \right)} \over {x\left( {{x^3} - 1} \right)}} \cr & Q = - {1 \over x} \cr} \) b. \({{2x - 6} \over {{x^3} - 3{x^2} - x + 3}} + Q = {6 \over {x - 3}} - {{2{x^2}} \over {1 - {x^2}}}\) \(\eqalign{ & Q = {6 \over {x - 3}} + {{2{x^2}} \over {{x^2} - 1}} - {{2x - 6} \over {{x^3} - 3{x^2} - x + 3}} \cr & Q = {6 \over {x - 3}} + {{2{x^2}} \over {{x^2} - 1}} - {{2x - 6} \over {\left( {x - 3} \right)\left( {{x^2} - 1} \right)}} \cr & Q = {{6\left( {{x^2} - 1} \right) + 2{x^2}\left( {x - 3} \right) - \left( {2x - 6} \right)} \over {\left( {x - 3} \right)\left( {{x^2} - 1} \right)}} \cr & Q = {{6{x^2} - 6 + 2{x^3} - 6{x^2} - 2x + 6} \over {\left( {x - 3} \right)\left( {{x^2} - 1} \right)}} = {{2{x^3} - 2x} \over {\left( {x - 3} \right)\left( {{x^2} - 1} \right)}} = {{2x\left( {{x^2} - 1} \right)} \over {\left( {x - 3} \right)\left( {{x^2} - 1} \right)}} \cr & Q = {{2x} \over {x - 3}} \cr} \) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 6. Phép trừ các phân thức đại số
|
-

Câu 30 trang 32 Sách bài tập (SBT) Toán 8 tập 1
Rút gọn biểu thức (chú ý dùng quy tắc đổi dấu để thấy nhân tử chung) :
-

Câu 31 trang 32 Sách bài tập (SBT) Toán 8 tập 1
Phân tích các tử thức và các mẫu thức (nếu cần thì dùng phương pháp thêm và bớt cùng một số hạng hoặc tách một số hạng thành hai số hạng) rồi rút gọn biểu thức :
-
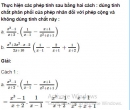
Câu 7.1 trang 33 Sách bài tập (SBT) Toán 8 tập 1
Thực hiện các phép tính sau bằng hai cách : dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này :

 Tải ngay
Tải ngay






