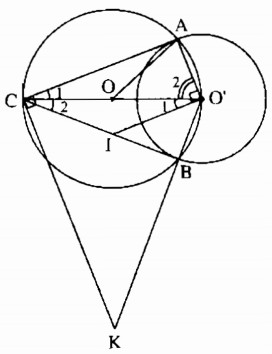
Câu 69 trang 168 Sách bài tập (SBT) Toán 9 Tập 1Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). a) Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (O’) b) Đường vuông góc với AO’ tại O’ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng. Giải:
a) Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O'AC} = 90^\circ \) Suy ra: CA ⊥ O’A tại điểm A Vậy CA là tiếp tuyến của đường tròn (O’) Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O'BC} = 90^\circ \) Suy ra: CB ⊥ O’B tại điểm B Vậy CB là tiếp tuyến đường tròn (O’) b) Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C. Suy ra: \(\widehat {ACO'} = \widehat {BCO'}\) (tính chất hai tiếp tuyến cắt nhau) Mà O’I ⊥ O’A (gt) CA ⊥ O’A (chứng minh trên) Suy ra: O’I // CA \( \Rightarrow \widehat {ACO'} = \widehat {CO'I}\) (hai góc so le trong) Suy ra: \(\widehat {BCO'} = \widehat {CO'I}\) Hay tam giác CIO’ cân tại I ⇒ IC = IO’ Khi đó I nằm trên đường trung trực của O’C Lại có: \(\widehat {AO'C} = \widehat {BO'C}\) (tính chất hai tiếp tuyến cắt nhau) KC ⊥ CA (gt) O’A ⊥ AC (chứng minh trên) Suy ra: KC // O’A \(\Rightarrow \widehat {AO'C} = \widehat {O'CK}\) (hai góc so le trong) Suy ra: \(\widehat {O'CK} = \widehat {KO'C}\) Hay tam giác CKO’ cân tại K ⇒ KC = KO’ Khi đó K nằm trên đường trung trực của O’C Mặt khác: OC = OO’ (= R) Suy ra O, I, K nằm trên đường trung trực của O’C. Vậy O, I, K thẳng hàng. Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 7. Vị trí tương đối của hai đường tròn
|
-
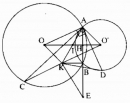
Câu 70 trang 168 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A
-
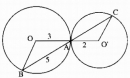
Câu 7.1 trang 168 Sách bài tập (SBT) Toán lớp 9 Tập 1
Cho h.bs.23, trong đó OA = 3, O'A = 2, AB = 5. Độ dài AC bằng:
-
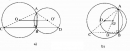
Câu 7.2 trang 168 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Một đường thẳng vuông góc với AB tại B cắt các đường tròn (O) và (O) theo thứ tự tại C và D ( khác B).
-
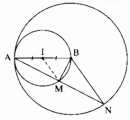
Câu 71 trang 168 Sách bài tập (SBT) Toán 9 Tập 1
Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I ; IA) và (B ; BA)

 Tải ngay
Tải ngay