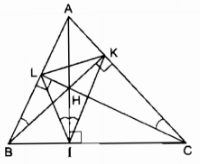
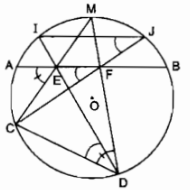
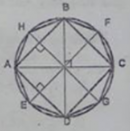
Câu 7.1, 7.2 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2Chứng minh IJ song song với AB. Câu 7.1 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2 Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. a) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L b) Chứng minh \(\widehat {LBH},\widehat {LIH},\widehat {KIH}\) và \(\widehat {KCH}\) là 4 góc bằng nhau. c) Chứng minh KB là tia phân giác của \(\widehat {LKI}\). Giải
Vì ∆ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC. a) Tứ giác AKHL có \(\widehat {AKH} + \widehat {ALH} = 90^\circ + 90^\circ = 180^\circ \) Tứ giác AKHL nội tiếp. Tứ giác BIHL có \(\widehat {BIH} + \widehat {BLH} = 90^\circ + 90^\circ = 180^\circ \) Tứ giác BIHL nội tiếp. Tứ giác CIHK có \(\widehat {CIH} + \widehat {CKH} = 90^\circ + 90^\circ = 180^\circ \) Tứ giác CIHK nội tiếp. Tứ giác ABIK có \(\widehat {AKB} = 90^\circ;\widehat {AIB} = 90^\circ \) K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có \(\widehat {BKC} = 90^\circ;\widehat {BLC} = 90^\circ \) K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp. Tứ giác ACIL có \(\widehat {AIC} = 90^\circ;\widehat {ALC} = 90^\circ \) I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp. b) Tứ giác BIHL nội tiếp. \( \Rightarrow \widehat {LBH} = \widehat {LIH}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{LH}\)) (1) Tứ giác CIHK nội tiếp. \( \Rightarrow \widehat {HIK} = \widehat {HCK}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{HK}\)) (2) Tứ giác BCKL nội tiếp. \( \Rightarrow \widehat {LBK} = \widehat {LCK}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{LK}\)) hay \(\widehat {LBH} = \widehat {HCK}\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {LKH} = \widehat {HKI}\). Vậy KB là tia phân giác của \(\widehat {LKI}.\) Câu 7.2 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2 Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB. Giải
M là điểm chính giữa của cung nhỏ \(\overparen{AB}\). \(\overparen{MA}\) = \(\overparen{MB}\) \(\widehat {AEC} = {1 \over 2}\) (sđ\(\overparen{AC}\) +sđ \(\overparen{MB}\)) (góc có đỉnh ở trong đường tròn) \(\widehat {CDM} = {1 \over 2}\) sđ\(\overparen{MAC}\) (tính chất góc nội tiếp) hay \(\widehat {CDF} = {1 \over 2}\) sđ\(\overparen{MA}\) + sđ\(\overparen{AC}\) Suy ra: \(\widehat {AEC} = \widehat {CDF}\) \(\widehat {AEC} + \widehat {{\rm{CEF}}} = 180^\circ \) (hai góc kề bù) Suy ra: \(\widehat {CDF} + \widehat {{\rm{CEF}}} = 180^\circ \) nên tứ giác CDFE nội tiếp \( \Rightarrow \widehat {CDE} = \widehat {CFE}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{CE}\)) hay \(\widehat {CDI} = \widehat {CFE}\) Trong đường tròn (O) ta có: \(\widehat {CDI} = \widehat {CJI}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{CAI}\)) Suy ra: \(\widehat {CJI} = \widehat {CFE}\) \( \Rightarrow \) IJ // AB (vì có cặp góc ở vị trí đồng tâm bằng nhau) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 7: Tứ giác nội tiếp
|
-
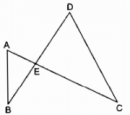
Câu 43 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2
Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

 Tải ngay
Tải ngay