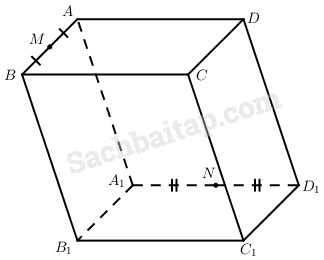
Câu 71 trang 128 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 71 trang 128 Sách bài tập Hình học 11 Nâng cao Cho M và N lần lượt là trung điểm của các cạnh AB, A1D1 của hình hộp ABCD.A1B1C1D1. a) Xác định giao điểm P và Q của mặt phẳng (CMN) với các đường thẳng B1C1 và DB1. b) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {AQ} \) qua các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) trong đó \(\overrightarrow b = \overrightarrow {AB} ,\overrightarrow c = \overrightarrow {A{\rm{D}}} ,\overrightarrow a = \overrightarrow {A{A_1}} \). Trả lời a) Đặt \(\overrightarrow {A{A_1}} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \). P là giao điểm của mp(CMN) với đường thẳng B1C1 khi và chỉ khi C, M, N, P thuộc một mặt phẳng và P thuộc đường thẳng B1C1. Ta có các điểm M, N, C, P thuộc một mặt phẳng nên tồn tại các số x, y, z sao cho: \(x + y + z = 1\,\,\,\,\,\,\,\,\,\,\,\left( * \right)\) và \(\overrightarrow {AP} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC.} \) Ta có: \(\eqalign{ & \overrightarrow {AP} = x.{{\overrightarrow b } \over 2} + y\left( {\overrightarrow a + {{\overrightarrow c } \over 2}} \right) + z\left( {\overrightarrow b + \overrightarrow c } \right) \cr & = y\overrightarrow a + \left( {{x \over 2} + z} \right)\overrightarrow b + \left( {{y \over 2} + z} \right)\overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr} \) Vì P thuộc đường thẳng B1C1 nên \(\overrightarrow {{B_1}P} = t\overrightarrow {{B_1}{C_1}} \), từ đó \(\overrightarrow {AP} = \overrightarrow b + \overrightarrow a +t \overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\) Từ (1), (2) và do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên \(\left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {**} \right)\) Kết hợp (*) và (**), ta có: \(\eqalign{ & \left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \cr & \Rightarrow z = - x \Rightarrow {x \over 2} - x = 1 \Leftrightarrow x = - 2 \cr & \Rightarrow z = 2,t = {5 \over 2} \cr} \) Vậy giao điểm của mp(CMN) với đường thẳng B1C1 là điểm P xác định bời \(\overrightarrow {{B_1}P} = {5 \over 2}\overrightarrow {{B_1}{C_1}} \) . Tương tự như trên, nếu gọi Q là giao điểm của mp(CMN) với đường thẳng B1D thì ta có \(x + y + z = 1\). và \(\eqalign{ & \overrightarrow {AQ} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC} \cr & = y\overrightarrow a + \left( {{x \over 2} + z} \right)\overrightarrow b + \left( {{y \over 2} + z} \right)\overrightarrow c \cr} \) Mặt khác \(\overrightarrow {AQ} = \overrightarrow b + \overrightarrow a + t\overrightarrow {{B_1}D}\) \( = \overrightarrow a + \overrightarrow b + t\left( { - \overrightarrow a - \overrightarrow b + \overrightarrow c } \right) \) \(= \left( {1 - t} \right)\overrightarrow a + \left( {1 - t} \right)\overrightarrow b + t\overrightarrow c\) Ta có hệ phương trình sau: \(\eqalign{ & \left\{ \matrix{ y = 1 - t \hfill \cr {x \over 2} + z = 1 - t \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x \over 2} - y + z = 0 \hfill \cr x + y + z = 1 \hfill \cr {x \over 2} + {y \over 2} + 2{\rm{z}} = 1 \hfill \cr} \right. \cr & \Rightarrow 1 - z = 2 - 4{\rm{z}} \Leftrightarrow z = {1 \over 3} \cr & \Rightarrow x = {2 \over 9},y = {4 \over 9},t = {5 \over 9}. \cr} \) Vậy giao điểm Q của đường thẳng B1D với mp(CMN) được xác định bởi \(\overrightarrow {{B_1}Q} = {5 \over 9}\overrightarrow {{B_1}D} \) b) Từ kết quả của câu a), ta có : \(\eqalign{ & \overrightarrow {AP} = \overrightarrow a + \overrightarrow b + {5 \over 2}\overrightarrow c \cr & \overrightarrow {AQ} = {4 \over 9}\overrightarrow a + {4 \over 9}\overrightarrow b + {5 \over 9}\overrightarrow c \cr} \). Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
|
-
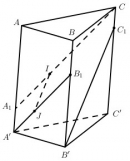
Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
-
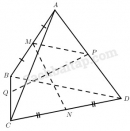
Câu 73 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 73 trang 128 Sách bài tập Hình học 11 Nâng cao
-
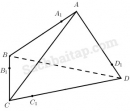
Câu 74 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 74 trang 128 Sách bài tập Hình học 11 Nâng cao
-
Câu 75 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 75 trang 128 Sách bài tập Hình học 11 Nâng cao

 Tải ngay
Tải ngay