Tải ngay
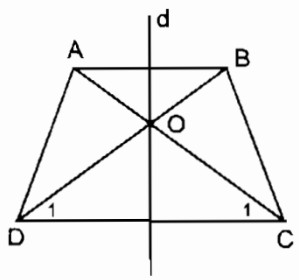
Câu 71 trang 88 Sách bài tập (SBT) Toán 8 tập 1Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân. Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân. Giải: Hình thang cân ABCD có AB // CD. Gọi O là giao điểm của hai đường chéo AC và BD. Xét ∆ ADC và ∆ BCD: AD = BC ( tính chất hình thang cân) AC = BD ( tính chất hình thang cân) CD cạnh chung Do đó ∆ ADC = ∆ BCD (c.c.c) \( \Rightarrow {\widehat D_1} = {\widehat C_1}\) ⇒ ∆ OCD cân tại O ⇒ OC = OD nên O nằm trên đường trung trực của CD. Trục đối xứng của hình thang cân là đường thẳng trung trực của hai đáy. Vậy O thuộc trục đối xứng của hình thang cân. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 6. Đối xứng trục
|
-
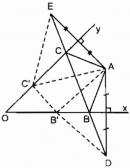
Câu 72 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
-
Câu 6.1 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Hãy nối mỗi cột của ô bên trái với một ô của cột bên phải để được khẳng định đúng.
-
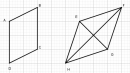
Câu 73 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?
