Tải ngay
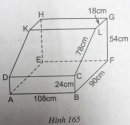
Câu 84 trang 156 Sách bài tập (SBT) Toán 8 tập 2Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình 164. Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình 164.
Giải: Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225\) Suy ra: BC = 15 (cm) Diện tích xung quanh bằng: \({S_{xq}} = \left( {9 + 12 + 15} \right).10 = 360(c{m^2})\) Diện tích mặt đáy bằng: \(S = {1 \over 2}.9.12 = 54(c{m^2})\) Diện tích toàn phần bằng: \({S_{TP}} = 360 + 2.54 = 468(c{m^2})\) c. Thể tích của hình lăng trụ bằng: \(V = S.h = 54.10 = 540(c{m^3})\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Ôn tập chương IV - Hình lăng trụ đứng. Hình chóp đều
|
-
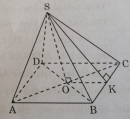
Câu 85 trang 156 Sách bài tập (SBT) Toán 8 tập 2
Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 10cm, chiều cao hình chóp là 12cm. Tính:
-
Câu 87 trang 157 Sách bài tập (SBT) Toán 8 tập 2
Thể tích của một hình chóp đều là 126cm3, chiều cao của hình chóp là 6cm. Như vậy: Trong các số dưới đây, số nào là diện tích đáy của nó ?
-
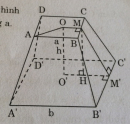
Câu 88 trang 157 Sách bài tập (SBT) Toán 8 tập 2
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ có các cạnh đáy là a và 2a, chiều cao của mặt bên là a.
