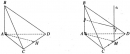
Đề 2 trang 135 Sách bài tập (SBT) Hình học 12Cho hình hộp chữ nhật OAIB.CEDF có tọa độ các đỉnh là A(3; 0 ; 0), B(0; 4; 0), C(0; 0; 5) và O(0; 0 ;0). ĐỀ 2 (45 PHÚT) Trang 135 sách bài tập (SBT) – Hình học 12 Cho hình hộp chữ nhật OAIB.CEDF có tọa độ các đỉnh là A(3; 0 ; 0), B(0; 4; 0), C(0; 0; 5) và O(0; 0 ;0). a) (2 điểm) Xác định tọa độ đỉnh D. Viết phương trình tổng quát của mặt phẳng (ABD). b) (2 điểm) Viết phương trình tham số của đường thẳng đi qua D và vuông góc với mặt phẳng (ABD). c) (3 điểm) Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD. d) (3 điểm) Tính khoảng cách giữa hai đường thẳng AC và EF. Hướng dẫn làm bài a) D(3; 4; 5) Ta có \(\overrightarrow {AD} = (0;4;5)\) và \(\overrightarrow {AB} = ( - 3;4;0)\) . Suy ra (ABD) có vecto pháp tuyến \(\overrightarrow n = \overrightarrow {AD} \wedge \overrightarrow {AB} = ( - 20; - 15;12)\) Phương trình của mặt phẳng (ABD) có dạng: \(20(x – 3) + 15y – 12z = 0\) hay \(20x +15y – 12z – 60 = 0\) b) Phương trình tham số của đường thẳng \(\Delta \) đi qua D và vuông góc với mặt phẳng (ABD): \(\left\{ {\matrix{{x = 3 + 20t} \cr {y = 4 + 15t} \cr {z = 5 - 12t} \cr} } \right.\) c) Mặt cầu (S) ngoại tiếp tứ diện ABCD cũng là mặt cầu ngoại tiếp tứ diện OABC. Giả sử phương trình của (S) là x2 + y2 + z2 + ax + by + cz + d = 0. Với điều kiện \({({a \over 2})^2} + {({b \over 2})^2} + {({c \over 2})^2} - d \ge 0\) (*) Vì (S) đi qua O, A, B, C nên thay tọa độ của O, A, B, C vào phương trình của (S) ta có :\(\left\{ {\matrix{{\matrix{{d = 0} \cr {9 + 3a = 0} \cr} } \cr {16 + 4b = 0} \cr {25 + 5c = 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{d = 0} \cr {a = - 3} \cr {b = - 4} \cr {c = - 5} \cr} } \right.\) thỏa mãn điều kiện (*) Vậy phương trình của (S) là x2 + y2 + z2 – 3x – 4y – 5z = 0 d) Ta có d(EF, AC) = d(EF, (ABC)) = d(E,(ABC)) \(\overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OC} = (3;0;5) \Rightarrow E(3;0;5)\) \(\overrightarrow {AB} = ( - 3;4;0),\overrightarrow {AC} = ( - 3;0;5)\) \(\Rightarrow \overrightarrow {AB} \wedge \overrightarrow {AC} = (20;15;12)\) Phương trình mặt phẳng (ABC) là \(20(x – 3) + 15y + 12z = 0\) hay \(20x + 15y + 12z – 60 = 0.\) Từ đó suy ra: \(d({\rm{EF}};AC) = {{|60 + 60 - 60|} \over {\sqrt {769} }} = {{60} \over {\sqrt {769} }}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
ĐỀ KIỂM TRA - CHƯƠNG III
|
-
Đề 3 trang 135 Sách bài tập (SBT) Hình học 12
Trong không gian Oxyz cho bốn điểm A(2; 4; -1),B(1; 4; -1),C(2; 4; 3), D(2; 2; -1).
-

Bài tập trắc nghiệm trang 38, 39 Sách bài tập (SBT) Giải tích 12
Hàm số dạng này có một điểm cực đại tại x = 0 và đồng biến trên khoảng (-∞; b) với b ≤ 0. Vậy hàm số đồng biến trên khoảng (-∞; 0).

 Tải ngay
Tải ngay







