Giải SGK Toán 11 Kết nối tri thức tập 2 trang 107, 108, 109Giải bài 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 trang 107, 108, 109 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,01 Bài 17 trang 106 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho mẫu số liệu ghép nhóm về thu thập của các công nhân tại một doanh nghiệp lớn:
Nhóm chứa mốt là A. \([5;10)\). B. \([10;15)\). C. \([15;20)\). D. \([20;25)\). Phương pháp: Nhóm có tần số lớn nhất gọi là nhóm chứa mốt Lời giải: Đáp án đúng là: C Tần số lớn nhất là 57 nên nhóm chứa mốt là [15; 20). Bài 18 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Vận động viên Tùng thi bắn súng. Biết rằng xác suất để Tùng bắn trúng vòng 10 là 0,2. Mỗi vận động viên được bắn hai lần và hai lần bắn là độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là A. 0,04 . B. 0,035 . C. 0,05 . D. 0,045 . Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Đáp án đúng là: A Gọi biến cố A: “Lần thứ nhất Tùng bắn trúng vòng 10”; Biến cố B: “Lần thứ hai Tùng bắn trúng vòng 10”. Biến cố C: “Tùng đạt huy chương vàng”. Theo đề có P(A) = 0,2; P(B) = 0,2. Ta có C = AB. Vì A, B là độc lập nên P(C) = P(A) . P(B) = 0,2 . 0,2 = 0,04. Vậy xác suất để Tùng đạt huy chương vàng là 0,04. Bài 19 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là A. \(\frac{{3}}{{4}}\). B. \(\frac{{25}}{{36}}\). C. \(\frac{{26}}{{35}}\). D. \(\frac{{28}}{{37}}\). Phương pháp: Công thức tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\) Lời giải: Đáp án đúng là: B Gọi biến cố A: “Số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1”. Khi đó ta có A = {(a,b)|a,b∈{2;3;4;5;6}}. Ta có n(A) = 25; n(Ω) = 36. P(A) = Vậy xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là Bài 20 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6. Xác suất để có ít nhất một bạn giành giải thưởng là A. 0,94 . B. 0,924 . C. 0,92 . D. 0,93 . Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Đáp án đúng là: C Gọi biến cố A: “An giành được giải thưởng”; Biến cố B: “Bình giành được giải thưởng”; A ∪">∪∪ B: “Có ít nhất một bạn được giải” Theo đề có P(A) = 0,8; P(B) = 0,6. Vì A, B độc lập nên ta có: P(AB) = P(A).P(B) = 0,8 . 0,6 = 0,48. Ta có P(A ∪">∪∪ B) = P(A) + P(B) – P(AB) = 0,8 + 0,6 – 0,48 = 0,92. Vậy xác suất để có ít nhất một bạn giành giải là 0,92. Bài 21 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Rút gọn các biểu thức sau: a) \(A = \frac{{1 - 2{{\sin }^2}x}}{{1 + \sin 2x}} - \frac{{1 - \tan x}}{{1 + \tan x}}\) b) \(B = \frac{{\sin 4x}}{{1 + \cos 4x}} \cdot \frac{{\cos 2x}}{{1 + \cos 2x}} - \cot \left( {\frac{{3\pi }}{2} - x} \right)\); c) \(C = 2\left( {{{\cos }^4}x - {{\sin }^4}x} \right)\sin 2x\). Phương pháp: Sử dụng các công thức lượng giác Lời giải:
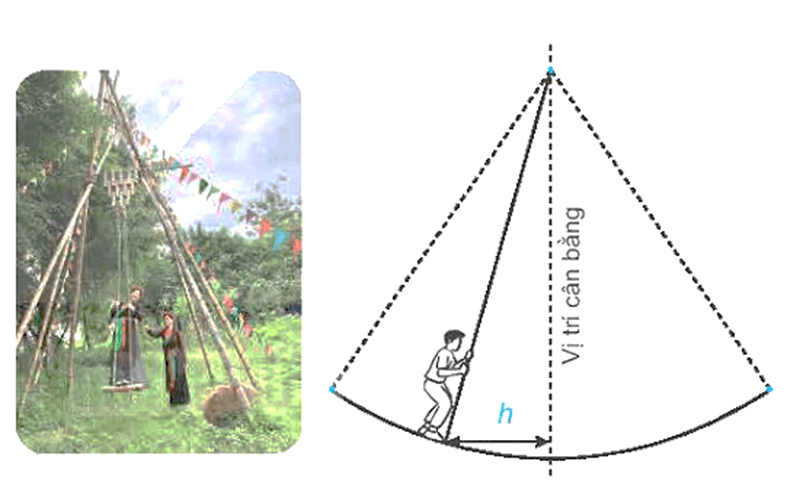
Bài 22 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị tri cân bằng. Giả sử khoảng cách \(h\) (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian \(t(t \ge 0\) và được tính bằng giây) bởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước rằng \(d > 0\) khi vị trí cân bằng ở về phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại.
a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất. b) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 m (tính chính xác đến 0,01 giây). Phương pháp: Sử dụng hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\) Lời giải:
Bài 23 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho cấp số nhân \(\left( {{u_n}} \right)\) biết rằng ba số \({u_1},{u_4}\) và \({u_7}\) lần lượt là các số hạng thứ nhất, thứ hai và thứ mười của một cấp số cộng có công sai \(d \ne 0\). Hãy tìm công bội \(q\) của cấp số nhân đó. Phương pháp: - Số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\) - Số hạng tổng quát của cấp số cộng \({u_n} = {u_1} + \left( {n - 1} \right)d\) Lời giải: Vì q là công bội của cấp số nhân (un) nên ta có: u4 = u1.q3 và u7 = u1.q6. Vì u1, u4 và u7 lần lượt là các số hạng thứ nhất, thứ hai và thứ mười của một cấp số cộng có công sai d ≠ 0 nên u4 = u1 + d; u7 = u1 + 9d. Ta có hệ Vì d ≠ 0 nên
Vậy q = 2. Bài 24 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một công ty đề xuất kí hợp đồng với một người lao động theo một trong hai loại hợp đồng sau: Hợp đồng A: Lương 200 triệu đồng cho năm đầu tiên và sau mỗi năm tăng thêm 10 triệu đồng. Hợp đồng B: Lương 180 triệu đồng cho năm đầu tiên và sau mối năm tăng thêm \(5\% \). Kí hiệu \({u_n},{v_n}\) tương ứng là lương nhận được (triệu đồng) của năm thứ \(n\) ứng với các hợp đồng A và B. a) Tính \({u_2},{u_3}\) và \({u_n}\) theo \(n\). Nếu người lao động đó làm việc cho công ty trong thời gian 5 năm theo hợp đồng A thì tổng số tiền lương người đó nhận được là bao nhiêu? b) Tính \({v_2},{v_3}\) và \({v_n}\) theo \(n\). Nếu người lao động đó làm việc cho công ty trong thời gian 5 năm theo hợp đồng B thì tổng số tiền lương người đó nhận được là bao nhiêu? c) Sau bao nhiêu năm thì lương hằng năm theo hợp đồng B vượt lương hằng năm theo hợp đồng A? Phương pháp: - Số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\) - Tổng cấp số nhân \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\) Lời giải: a) Ta có u2 = u1 + 10 = 200 + 10 = 210 triệu đồng; u3 = u2 + 10 = 210 + 10 = 220 triệu đồng. Ta thấy un là một cấp số cộng với u1 = 200 và d = 10 nên un = u1 + (n – 1)d = 200 + (n – 1)10 = 10n + 190. Nếu người lao động đó làm việc cho công ty trong thời gian 5 năm theo hợp đồng A thì tổng số tiền lương người đó nhận được là: S5(A) = u1 + u2 + …+ u5 = b) Ta có v2 = v1 + 5%.v1 = v1 . 1,05 = 180 . 1,05 = 189 (triệu đồng); v3 = v2 + v2.5% = v2 .1,05 = 189 . 1,05 = 198,45 (triệu đồng). Ta thấy vn là một cấp số nhân với v1 = 180 và q = 1,05 nên vn = v1 . (1,05)n – 1 = 180 . (1,05)n – 1. Nếu người lao động đó làm việc cho công ty trong thời gian 5 năm theo hợp đồng B thì tổng số tiền lương người đó nhận được là: S5(B) = v1 + v2 + …+ v5 = c) Để lương hàng năm theo hợp đồng B vượt lương hằng năm theo hợp đồng A thì vn > un hay 180.(1,05)n – 1 > 10n + 190 ⇔ 18 . (1,05)n – 1 > n + 19. Ta thấy n = 13 là số nguyên dương nhỏ nhất thỏa mãn bất phương trình này nên từ năm thứ 13 trở đi thì lương hằng năm theo hợp đồng B vượt lương hằng năm theo hợp đồng A. Bài 25 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính các giới hạn sau: a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 + 3 + 5 + \cdots + (2n - 1)}}{{{n^2} + 2n + 3}}\). b) \(\mathop {\lim }\limits_{n \to + \infty } \left( {1 + \frac{2}{3} + \frac{4}{9} + \cdots + \frac{{{2^n}}}{{{3^n}}}} \right)\); c) \(\mathop {\lim }\limits_{x \to - 2} \frac{{2{x^2} + 3x - 2}}{{{x^2} - 4}}\) d) \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {4{x^2} + x + 1} + 2x} \right)\). Phương pháp: - Sử dụng các quy tắc, một số giới hạn đặc biệt để tìm giới hạn - Tổng cấp số cộng \({S_n} = \frac{{{u_1} + {u_n}}}{2}.n\) - Tổng cấp số nhân \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\) Lời giải: a) Ta có 1; 3; 5; …; 2n – 1 là một cấp số cộng có Suy ra 1 + 3 + 5 + … + (2n – 1) = Khi đó b) Ta có 1;23;49;...;2n3n">1;23;49;...;2n3n">1; Khi đó
Bài 26 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tìm các giá trị của tham số \(m\) để: a) Hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} + 4x + 3}}{{x + 1}}}&{{\rm{ khi }}x \ne - 1}\\{{m^2}}&{{\rm{ khi }}x = - 1}\end{array}} \right.\) liên tục tại điểm \(x = - 1\); b) Hàm số \(g(x) = \left\{ {\begin{array}{*{20}{l}}{2x + m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi }}x \le 1}&{\rm{ }}\\{\frac{{{x^3} - {x^2} + 2x - 2}}{{x - 1}}{\rm{ }}\,{\rm{khi }}x > 1}&{}\end{array}} \right.\)liên tục trên \(\mathbb{R}\). Phương pháp: Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Lời giải: a) Ta có Để hàm số liên tục tại x = −1 thì Vậy m=±2">m= b) Ta có x < 1 thì g(x) = 2x + m liên tục với mọi x < 1. Có x > 1 thì g(x) = Tại x = 1, ta có:
Có g(1) = 2 ∙ 1 + m = 2 + m. Hàm số đã cho liên tục trên ℝ khi và chỉ khi hàm số liên tục tại x = 1
Vậy m = 1 thì hàm số đã cho liên tục trên ℝ. Bài 27 trang 107 SGK Toán 11 - Kết Nối Tri Thức tập 2 Giải các phương trình và bất phương trình sau: a) \({3^{\frac{1}{x}}} = 4\) b) \({2^{{x^2} - 3x}} = 4\); c) \({\log _4}(x + 1) + {\log _4}(x - 3) = 3\); d) \({\left( {\frac{1}{5}} \right)^{{x^2} - 2x}} \ge \frac{1}{{125}}\) e) \({(2 - \sqrt 3 )^x} \le {(2 + \sqrt 3 )^{x + 2}}\) f) \(\log \left( {3{x^2} + 1} \right) > \log (4x)\). Phương pháp: Tìm điều kiện của các phương trình sau đó giải Lời giải: a) Điều kiện: x ≠ 0. Ta có Vậy nghiệm của phương trình là x = log43.
Vậy tập nghiệm của phương trình là S = c) Điều kiện Ta có log4 (x + 1) + log4 (x – 3) = 3 ⇔ log4 [(x + 1)(x – 3)] = 3 ⇔ (x + 1)(x – 3) = 43 ⇔ x2 – 2x – 67 = 0 ⇔ x = 1 - 2 Vậy nghiệm của phương trình là x = 1 + 2 d) Ta có:
Vậy tập nghiệm của bất phương trình là S = [−1; 3].
Vậy tập nghiệm của bất phương trình là S = [−1; +∞). f) Điều kiện: 4x > 0 ⇔ x > 0. Ta có log (3x2 + 1) > log (4x) ⇔ 3x2 + 1 > 4x ⇔ 3x2 – 4x + 1 > 0 ⇔">⇔ Kết hợp với điều kiện, ta có Vậy tập nghiệm của bất phương trình là S=(0; Bài 28 trang 108 SGK Toán 11 - Kết Nối Tri Thức tập 2 Để xác định tính acid và tính bazơ của các dung dịch, người ta sử dụng khái niệm độ \({\rm{pH}}\). Độ \({\rm{pH}}\) của một dung dịch được cho bởi công thức \({\rm{pH}} = - \log \left[ {{{\rm{H}}^ + }} \right]\), trong đó \(\left[ {{{\rm{H}}^ + }} \right]\) là nồng độ của ion hydrogen (tính bằng mol/lít). a) Tính độ pH của một dung dịch có nồng độ ion hydrogen là 0,1 mol/ít. b) Độ pH sẽ biến đổi như thế nào nếu nồng độ ion hydrogen giảm? c) Xác định nồng độ ion hydrogen trong bia biết độ \({\rm{pH}}\) của bia là khoảng 4,5. Phương pháp: Sử dụng công thức \({\rm{pH}} = - \log \left[ {{{\rm{H}}^ + }} \right]\) Lời giải: a) Độ pH của một dung dịch có nồng độ ion hydrogen là 0,1 mol/lít là pH = −log0,1 = 1. Vậy độ pH của một dung dịch có nồng độ ion hydrogen là 0,1 mol/lít là 1. b) Vì hàm số y = log x đồng biến trên khoảng (0; +∞">∞∞) nên hàm số y = −log x nghịch biến trên (0; +∞">∞∞). Suy ra nếu nồng độ ion hydrogen giảm thì độ pH sẽ tăng. c) Có pH = 4,5 nên −log[H+] = 4,5 ⇔ [H+] = 10−4,5. Vậy nồng độ ion hydrogen trong bia là 10−4,5 mol/lít. Bài 29 trang 108 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính đạo hàm của các hàm số sau: a) \(y = 3{x^2} - 2\sqrt x \); b) \(y = \sqrt {1 + 2x - {x^2}} \); c) \(y = \tan \frac{x}{2} - \cot \frac{x}{2}\) d) \(y = {e^{ex}} + \ln {x^2}\). Phương pháp: Sử dụng các công thức và quy tắc để tính đạo hàm. Lời giải: a) Ta có: b) Ta có:
Bài 30 trang 108 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một chất điểm chuyển động có phương trình \(s(t) = {t^3} - 3{t^2} - 9t + 2\), ở đó thời gian \(t > 0\) tính bằng giây và quãng đường \(s\) tính bằng mét. a) Tính vận tốc của chất điểm tại thời điểm \(t = 2\) giây. b) Tính gia tốc của chất điểm tại thời điểm \(t = 3\) giây. c) Tính gia tốc của chất điểm tại thời điểm vận tốc bằng 0. d) Tính vận tốc của chất điểm tại thời điểm gia tốc bằng 0. Phương pháp: Ý nghĩa vật lý của đạo hàm \(v = s',a = s''\) Lời giải: Vận tốc của chất điểm tại thời điểm t là v(t) = s'(t) = 3t2 – 6t – 9. Gia tốc của chất điểm tại thời điểm t là a(t) = v'(t) = 6t – 6. a) Vận tốc của chất điểm tại thời điểm t = 2 giây là v(2) = 3 . 22 – 6 . 2 − 9 = −9 (m/s). b) Gia tốc của chất điểm tại thời điểm t = 3 giây là a(3) = 6 . 3 – 6 = 12 (m/s2). c) Vận tốc bằng 0 tức là v(t) = 0 ⇔ 3t2 – 6t – 9 = 0 ⇔ t = 3 (thỏa mãn) hoặc t = −1 (loại). Vậy gia tốc của chất điểm tại thời điểm vận tốc bằng 0 là a(3) = 12 m/s2. d) Gia tốc bằng 0 tức là a(t) = 0 ⇔ 6t – 6 = 0 ⇔ t = 1. Vậy vận tốc của chất điểm tại thời điểm gia tốc bằng 0 là v(1) = 3 . 12 – 6 . 1 – 9 = −12 m/s. Bài 31 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho tứ diện OABC có \(OA = OB = OC = a,\widehat {AOB} = \widehat {AOC} = {60^0}\) và \(\widehat {BOC} = {90^0}\). a) Chứng minh rằng \((OBC) \bot (ABC)\). b) Tính theo a khoảng cách từ \(O\) đến mặt phẳng \((ABC)\) và thể tích khối tứ diện OABC. Phương pháp: - Hai mặt phẳng được gọi là vuông góc nếu trong mặt phẳng này có 1 đường vuông góc với mặt phẳng kia. - Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a. - Thể tích khối tứ diện \(V = \frac{1}{3}h.S\) Lời giải:
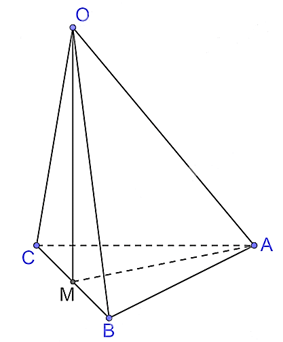 a) Gọi M là trung điểm của BC. Xét tam giác OBC có OB = OC = a nên tam giác OBC cân tại O mà OM là trung tuyến nên OM đồng thời là đường cao hay OM ⊥ BC. Vì tam giác OAC có OA = OC = a và Vì tam giác OAB có OA = OB = a và Xét tam giác OBC vuông tại O, có BC = Xét tam giác OBC vuông tại O, OM là đường cao, có
Vì BC2 = 2a2 = a2 + a2 = AB2 + AC2 nên tam giác ABC vuông tại A. Mặt khác AB = AC nên tam giác ABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao hay AM ⊥ BC. Xét tam giác ABC vuông tại A, AM là đường cao có:
Vì OA2 = Vì OM ⊥ MA và OM ⊥BC nên OM ⊥ (ABC) mà OM ⊂ (OBC), suy ra (OBC) ⊥ (ABC). b) Vì OM ⊥ (ABC) nên d(O, (ABC)) = OM =
Bài 32 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chóp \(S.ABCD\) có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD)\) và \(SA = a\sqrt 2 \). Mặt phẳng \((P)\) đi qua điểm \(A\) và vuông góc với đường thẳng SC, cắt các cạnh SC, SB, SD lần lượt tại M, E, F. a) Chứng minh rằng \(AE \bot (SBC)\). b) Tính theo a thể tích khối chóp S.ABCD và hình chóp S.AEMF. Phương pháp: - Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó. - Tỉ số thể tích \(\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}\) Lời giải:
a) Gọi O là giao điểm của AC và BD. Kẻ AM ⊥ SC tại M, SO ∩ AM = I. Do ABCD là hình vuông nên AC ⊥ BD. Vì SA ⊥ (ABCD) nên SA ⊥ BD mà AC ⊥ BD nên BD ⊥ (SAC), suy ra BD ⊥ SC. Trong mặt phẳng (SBD), qua I kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại E và F. Khi đó (P) = (AEMF). Do ABCD là hình vuông nên BC ⊥ AB, SA ⊥ BC (do SA ⊥ (ABCD)) nên BC ⊥ (SAB), suy ra BC ⊥ AE. Mặt khác SC ⊥ (P) nên SC ⊥ AE mà BC ⊥ AE nên AE ⊥ (SBC). b) Ta có Xét tam giác SAB vuông tại A, có Xét tam giác SAD vuông tại A, có Xét tam giác ABC vuông tại B, có Vì SA ⊥ (ABCD) nên SA ⊥ AC hay tam giác SAC vuông tại A. Xét tam giác SAC vuông tại A, có Có AE ⊥ (SBC) nên AE ⊥ SB. Xét tam giác SAB vuông tại A, AE là đường cao nên SA2 = SE . SB. Có Xét tam giác SAC vuông tại A, AM là đường cao nên SA2 = SM.SC. Có Do ABCD là hình vuông nên DC ⊥ AD mà SA ⊥ DC (do SA ⊥ (ABCD)) nên DC ⊥(SAD), suy ra DC ⊥ AF. Mặt khác SC ⊥ (P) nên SC ⊥ AF mà DC ⊥ AF nên AF ⊥(SCD), suy ra AF ⊥ SD. Xét tam giác SAD vuông tại A, AF là đường cao nên SA2 = SF . SD. Bài 33 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a,AA' = a\sqrt 2 \). Gọi M, N lần lượt là trung điểm của cạnh \(BB'\) và \(CC'\). Mặt phẳng \(\left( {A'MN} \right)\) cắt đường thẳng AB, AC tương ứng tại \(H\) và \(K\). a) Chứng minh rằng \(MN//HK\). b) Tính theo a thể tích khối chóp \(A'\).AHK. Phương pháp: Thể tích khối chóp \(V = \frac{1}{3}h.S\) Lời giải:
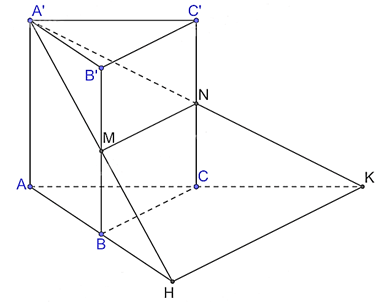
a) Vì M, N lần lượt là trung điểm của cạnh BB' và CC' nên MN // BC, suy ra MN // (ABC). Mà (ABC) ∩ (A'MN) = HK, suy ra MN // HK. b) Xét ∆ A'B'M và ∆HBM có B'M = BM (do M là trung điểm của BB'),
Do đó, ∆A'B'M = ∆HBM. Suy ra BH = A'B' mà AB = A'B' (do ABB'A' là hình chữ nhật) nên BH = AB = a. Suy ra AH = 2a. Xét ∆A'C'N và ∆KCN có C'N = CN (do N là trung điểm của CC'),
Do đó, ∆A'C'N = ∆KCN, suy ra CK = A'C' mà A'C' = AC (do ACC'A' là hình chữ nhật) nên CK = AC = a, suy ra AK = 2a. Xét tam giác AHK có B là trung điểm AH, C là trung điểm AK nên BC là đường trung bình của tam giác AHK, suy ra HK = 2BC = 2a. Xét tam giác AHK có AH = AK = HK = 2a nên tam giác AHK đều, suy ra
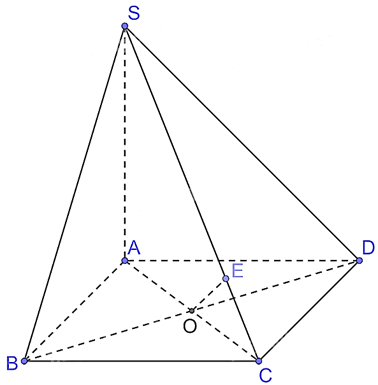
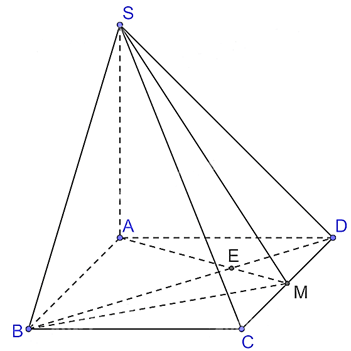
Bài 34 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \(\widehat {BAD} = {60^0}\). Biết \(SA \bot (ABCD)\) và \(SA = a\). a) Chứng minh rằng \(BD \bot SC\). b) Tính theo a khoảng cách giữa hai đường thẳng BD và SC. Phương pháp: Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b. Lời giải:
a) Vì ABCD là hình thoi nên AC ⊥ BD. Vì SA ⊥ (ABCD) nên SA ⊥ BD mà AC ⊥ BD nên BD ⊥ (SAC), suy ra BD ⊥ SC. b) Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC, BD. Kẻ OE ⊥ SC tại E. Vì BD ⊥ (SAC) nên BD ⊥ OE mà OE ⊥ SC nên d(BD, SC) = OE. Xét tam giác ABD có AB = AD = a nên tam giác ABD cân tại A mà Xét tam giác đều ABD cạnh a có AO là đường cao nên AO = Vì SA ⊥ (ABCD) nên SA ⊥ AC hay tam giác SAC vuông tại A. Xét tam giác SAC vuông tại A, có Vì O là trung điểm của AC nên CO = AO = Xét ∆CEO và ∆CAS có:
Vậy d(BD, SC) = Bài 35 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, \(AD = a,AB = a\sqrt 2 \). Biết \(SA \bot (ABCD)\) và \(SA = a\sqrt 3 \). Gọi \(M\) là trung điểm của cạnh CD. a) Chứng minh rằng \(BD \bot (SAM)\). b) Tính theo a thể tích khối chóp S.ABMD. Phương pháp: Thể tích khối chóp \(V = \frac{1}{3}h.S\) Lời giải:
a) Do ABCD là hình chữ nhật nên AB = DC = Gọi E là giao điểm của AM và BD. Vì M là trung điểm của CD nên DM = MC = Xét tam giác ADM vuông tại D có: Xét tam giác ADB vuông tại A có:
Vì SA⊥ (ABCD) nên SA ⊥ BD mà AM ⊥ BD nên BD ⊥(SAM). b) Có SABMD = SABCD – SBCM = AB.AD -
Bài 36 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Trong đại dịch Covid-19, một doanh nghiệp muốn hỗ trợ các gia đình thuộc nhóm \(25\% \) hộ gia đình có thu nhập thấp nhất ở một địa phương. Một mẫu số liệu ghép nhóm về thu nhập của các hộ gia đình ở địa phương này được cho trong bảng sau:
Dựa trên mẫu số liệu trên, hãy xác định hộ gia đình có thu nhập dưới bao nhiêu sẽ nhận được hỗ trợ của doanh nghiệp đó? Phương pháp: Để tính tứ phân vị thứ nhất Q1 của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa Q1, giả sử đó là nhóm thứ \(p:\left[ {{a_p};{a_{p + 1}}} \right).\) Khi đó, \({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + ... + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right),\) Trong đó, n là cỡ mẫu, mp là tần số nhóm p, với p = 1 ta quy ước m1 +…+ mp-1 = 0. Lời giải: Dựa vào bảng số liệu, ta tính được n = 8 + 17 + 35 + 56 + 27 + 15 = 158. Giả sử x1; x2; …; x158 là mẫu số liệu đã được sắp xếp theo thứ tự không giảm. Khi đó trung vị là Do đó, nhóm chứa tứ phân vị thứ nhất Q1 là nhóm thứ 3: [8; 11). Có a3 = 8; m3 = 35; m1 = 8; m2 = 17; a4 = 11. Áp dụng công thức tính tứ phân vị thứ nhất Q1, ta có:
Vậy doanh nghiệp sẽ hỗ trợ hộ gia đình có thu nhập dưới 9,24 triệu đồng. Bài 37 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hai bạn Dũng và Cường tham gia một kì thi học sinh giỏi môn Toán. Xác suất để Dũng và Cường đạt giải tương ứng là 0,85 và 0,9 . Tính xác suất để: a) Có ít nhất một trong hai bạn đạt giải; b) Có đúng một bạn đạt giải. Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Gọi biến cố A: “Dũng đạt giải”; Biến cố B: “Cường đạt giải”; A ∪ B: “Có ít nhất một bạn được giải”.
Theo đề, có P(A) = 0,85; P(B) = 0,9. Vì A, B độc lập nên P(AB) = P(A) . P(B) = 0,85 . 0,9 = 0,765.
a) Ta cần tính P(A ∪ B). Biến cố đối của biến cố “Có ít nhất một bạn được giải” là biến cố “Không có bạn nào đạt giải” nên ta có Vậy xác suất để có ít nhất một trong hai bạn đạt giải là 0,985. b) Gọi biến cố E: “Có đúng một bạn đạt giải”. Ta có E = Do đó P(E) =
= 0,85 . (1 – 0,9) + (1 – 0,85) . 0,9 = 0,22. Vậy xác suất để có đúng một bạn đạt giải là 0,22. Bài 38 trang 109 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,015. Các động cơ hoạt động độc lập với nhau. Tính xác suất để chuyến bay hạ cánh an toàn. Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Gọi biến cố E: “Cánh phải có ít nhất một động cơ không bị lỗi”; Biến cố F: “Cánh trái có ít nhất một động cơ không bị lỗi”; Biến cố Biến cố Biến cố M: “Chuyến bay hạ cánh an toàn”. Vì các động cơ hoạt động độc lập với nhau nên ta có: P( Suy ra P(E) = 1-P( Vì E, F là các biến cố độc lập nên P(M) = P(EF) = P(E) . P(F) = 0,9999 . 0,999775 ≈ 0,9997. Vậy xác suất để chuyến bay đó hạ cánh an toàn khoảng 0,9997. Sachbaitap.com
Xem thêm tại đây:
BÀI TẬP ÔN TẬP CUỐI CUỐI NĂM
|

 Tải ngay
Tải ngay
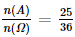
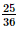

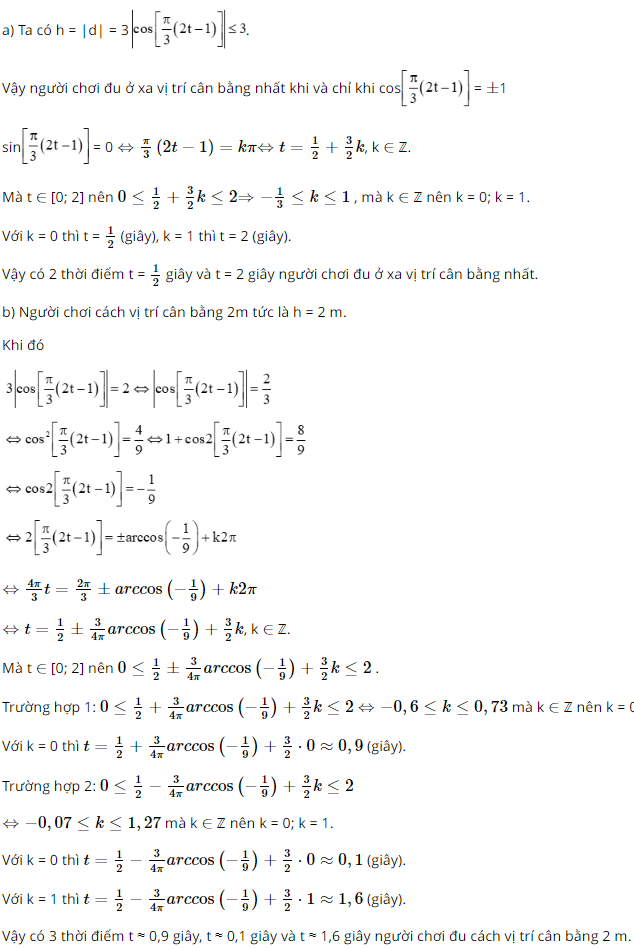
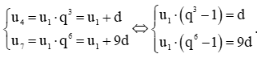
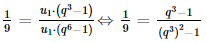
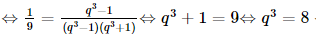
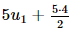 .d= 5 . 200 + 100 = 1 100 (triệu đồng).
.d= 5 . 200 + 100 = 1 100 (triệu đồng).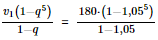 ≈ 994,61 triệu đồng.
≈ 994,61 triệu đồng.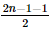
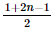
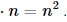
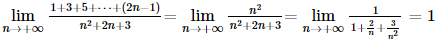
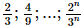
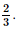
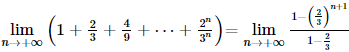
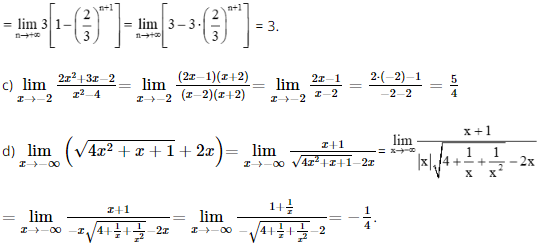
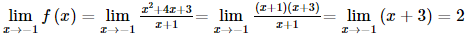 ; f(−1) = m2.
; f(−1) = m2.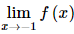
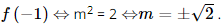
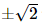
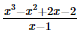
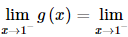
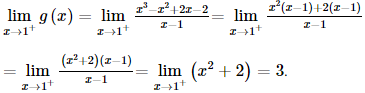
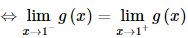
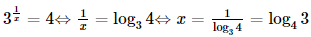
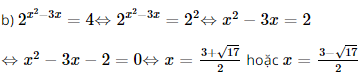
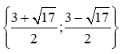
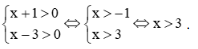
 (thỏa mãn).
(thỏa mãn).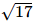 .
.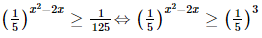
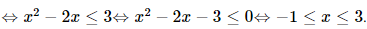
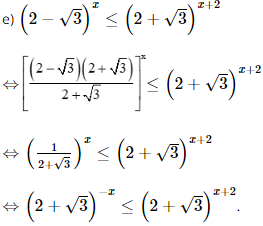
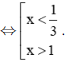
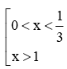
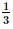
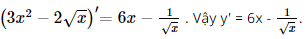
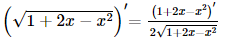
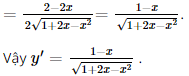
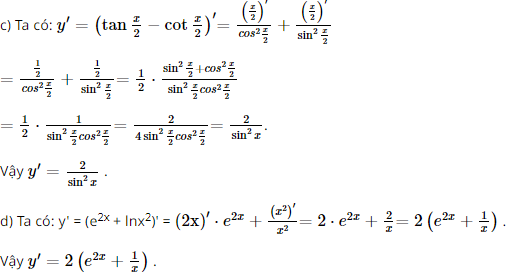
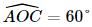 nên tam giác OAC đều, suy ra AC = a.
nên tam giác OAC đều, suy ra AC = a.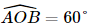 nên tam giác OAB đều, suy ra AB = a.
nên tam giác OAB đều, suy ra AB = a.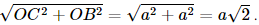
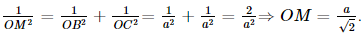
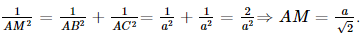
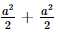 = OM2 + AM2 nên tam giác OMA vuông tại M, suy ra OM ^ MA.
= OM2 + AM2 nên tam giác OMA vuông tại M, suy ra OM ^ MA.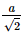
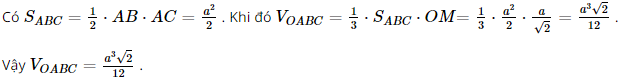

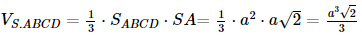
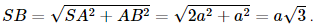 .
.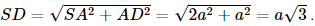 .
.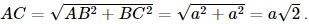 .
.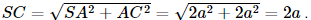
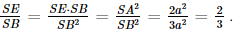
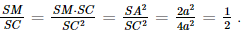
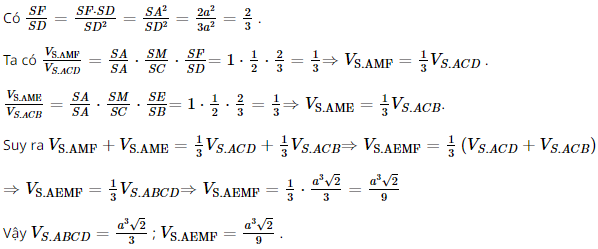
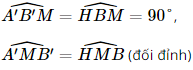
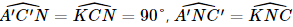
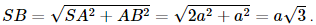
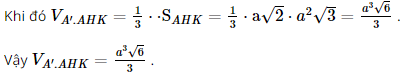
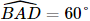 nên tam giác ABD đều.
nên tam giác ABD đều.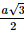
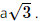
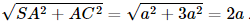
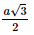
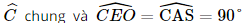
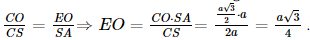
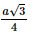
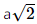 ; AD = BC = a.
; AD = BC = a.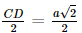
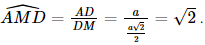 .
.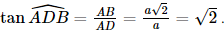
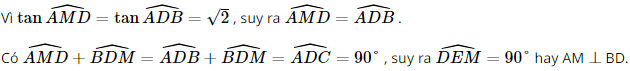
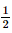 .
.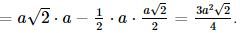
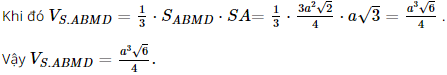

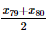 và tứ phân vị thứ nhất là x40.
và tứ phân vị thứ nhất là x40.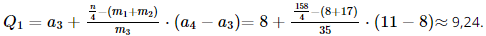
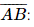 : “Không có bạn nào đạt giải”;
: “Không có bạn nào đạt giải”;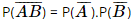
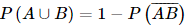
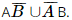 Do A và B độc lập nên A và
Do A và B độc lập nên A và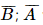 và B cũng độc lập.
và B cũng độc lập.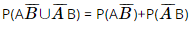
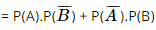
 : “Cả hai động cơ ở cánh phải đều bị lỗi”;
: “Cả hai động cơ ở cánh phải đều bị lỗi”;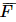 : “Cả hai động cơ ở cánh trái đều bị lỗi”.
: “Cả hai động cơ ở cánh trái đều bị lỗi”.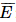 ) = 0,01.0,01 = 10
) = 0,01.0,01 = 10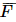 ) = 0,015.0,015 = 2,25.10
) = 0,015.0,015 = 2,25.10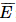 ) = 0,9999; P(F) = 1 - P(
) = 0,9999; P(F) = 1 - P(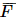 ) = 0,999775.
) = 0,999775.