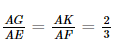Giải SGK Toán 11 Kết nối tri thức tập 2 trang 30Giải bài 7.1, 7.2, 7.3, 7.4 trang 30 SGK Toán lớp 11 Kết Nối Tri Thức tập 2.Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau? Bài 7.1 trang 30 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình lăng trụ ABC.A'B'C' có các đáy là các tam giác đều. Tính góc (AB, B'C').
Phương pháp: Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có đường thẳng b' song song với b. Khi đó (a, b) = (a', b') Lời giải: Do ABC.A'B'C' là hình lăng trụ nên các mặt bên là hình bình hành. Do ABB'A' là hình bình hành nên AB // A'B'. Khi đó (AB, B'C') = (A'B', B'C') = Do tam giác A'B'C' là tam giác đều nên Vậy (AB, B'C') = 60°. Bài 7.2 trang 30 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.
Phương pháp: Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b. Lời giải: Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên các mặt của hình hộp là hình thoi. Vì ABB'A' là hình thoi nên AB' ^ A'B. Có CB // A'D' và CB = A'D' (do cùng song song và bằng AD). Do đó CBA'D' là hình bình hành, suy ra CD' // BA'.
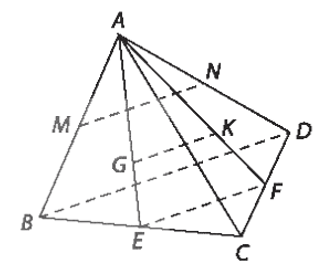
Khi đó (CD', AB') = (BA', AB') = 90°. Vậy CD' và AB' vuông góc với nhau. Vì ADD'A' là hình thoi nên AD' ^ A'D. Có CD // A'B' và CD = A'B' (vì CD, A'B' cùng song song và bằng AB) nên CDA'B' là hình bình hành, suy ra CB' // DA'. Khi đó (CB', AD') = (DA', AD') = 90°. Vậy CB' và AD' vuông góc với nhau. Do ABCD là hình thoi nên AC ^ BD. Vì BB' // DD' và BB' = DD' (do BB', DD' cùng song song và bằng AA' ) nên BDD'B' là hình bình hành, suy ra BD // B'D'. Khi đó (AC, B'D') = (AC, BD) = 90°. Vậy AC và B'D' vuông góc với nhau. Bài 7.3 trang 30 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\) a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc BC. b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC. Phương pháp: Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b. Lời giải:
a) Xét tam giác ABD, có M là trung điểm của AB, N là trung điểm của AD nên MN là đường trung bình của tam giác ABD, suy ra MN // BD. Khi đó (MN, BC) = (BD, BC) = Vậy MN vuông góc với BC. b) Gọi AG cắt BC tại E, suy ra E là trung điểm BC, AK cắt CD tại F, suy ra F là trung điểm CD. Vì G là trọng tâm tam giác ABC nên Xét tam giác AEF có Xét tam giác BCD có E, F lần lượt là trung điểm của BC, CD nên EF là đường trung bình, suy ra EF // BD. Vì GK // EF và EF // BD nên GK // BD mà BD ⊥ BC nên GK ⊥ BC. Bài 7.4 trang 30 SGK Toán 11 - Kết Nối Tri Thức tập 2 Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau?
Phương pháp: Hai đường thẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng 900. Lời giải: Những cặp đường thẳng sau vuông góc với nhau: hoành (1) và quá giang (2); hoành (1) và rui (4); hoành (1) và cột (5); quá giang (2) và xà cái (3); quá giang (2) và cột (5); xà cái (3) và rui (4); xà cái (3) và cột (5). Sachbaitap.com
Xem thêm tại đây:
Bài 22. Hai đường thẳng vuông góc
|
-

Giải SGK Toán 11 Kết nối tri thức tập 2 trang 36
Giải bài 7.5, 7.6, 7.7, 7.8, 7.9 trang 36 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ( bot ) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng: a) BC ( bot ) (SAM); b) Tam giác SBC cân tại S.

 Tải ngay
Tải ngay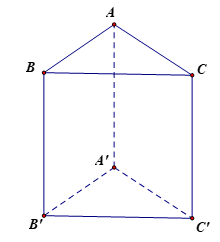
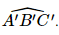 .
.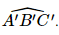

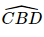 =
=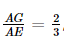 , K là trọng tâm tam giác ACD nên
, K là trọng tâm tam giác ACD nên 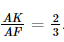 .
.