Giải SGK Toán 11 Kết nối tri thức tập 2 trang 36

Bài 7.5 trang 36 SGK Toán 11 - Kết Nối Tri Thức tập 2

Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA \( \bot \) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:

a) BC \( \bot \) (SAM);

b) Tam giác SBC cân tại S.

Phương pháp:

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Lời giải:

a) Vì SA ⊥ (ABC) nên SA ⊥ BC.

Vì ABC là tam giác cân tại A, AM là trung tuyến nên AM là đường cao hay AM ⊥ BC.

Do SA ⊥ BC và AM ⊥ BC nên BC ⊥ (SAM).

b) Vì BC ⊥ (SAM) nên BC ⊥ SM.

Xét tam giác SBC có SM là trung tuyến đồng thời là đường cao nên tam giác SBC cân tại S.

Bài 7.6 trang 36 SGK Toán 11 - Kết Nối Tri Thức tập 2

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA \( \bot \) (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.

Phương pháp:

- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

- Định nghĩa đường thẳng vuông góc mặt phẳng.

Lời giải:

Vì SA ⊥ (ABCD) nên SA ⊥ AD, SA ⊥ AB, SA ⊥ BC, SA ⊥ CD.

Do ABCD là hình chữ nhật nên AB ⊥ BC, AD ⊥ DC.

Vì SA ⊥ AB nên tam giác SAB vuông tại A.

Vì SA ⊥ AD nên tam giác SAD vuông tại A.

Vì SA ⊥ BC và AB ⊥ BC nên BC ⊥ (SAB), suy ra BC ⊥ SB hay tam giác SBC vuông tại B.

Vì SA ⊥ CD và AD ⊥ DC nên CD ⊥ (SAD), suy ra CD ⊥ SD hay tam giác SCD vuông tại D.

Bài 7.7 trang 36 SGK Toán 11 - Kết Nối Tri Thức tập 2

Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA \( \bot \) (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng:

AM \( \bot \) (SBC), AN \( \bot \) (SCD), SC \( \bot \) (AMN).

Phương pháp:

- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

- Định nghĩa đường thẳng vuông góc mặt phẳng.

Lời giải:

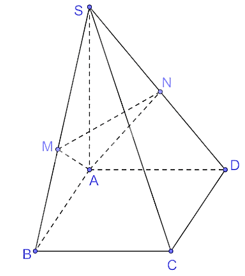
- Vì SA ⊥ (ABCD) nên SA ⊥ BC.

Do ABCD là hình chữ nhật nên BC ⊥ AB mà SA ⊥ BC nên BC ⊥ (SAB), suy ra BC ⊥ AM.

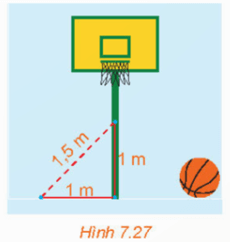
Vì AM ⊥ SB và BC ⊥ AM nên AM ⊥ (SBC).

- Vì SA ⊥ (ABCD) nên SA ⊥ CD.

Do ABCD là hình chữ nhật nên AD ⊥ CD.

Vì AD ⊥ CD và SA ⊥ CD nên CD ⊥ (SAD), suy ra CD ⊥ AN.

Do N là hình chiếu của A trên SD nên AN ⊥ SD.

Vì AN ⊥ SD và CD ⊥ AN nên AN ⊥ (SCD).

- Do AM ⊥ (SBC) nên AM ⊥ SC và AN ⊥ (SCD) nên AN ⊥ SC.

Vì AM ⊥ SC và AN ⊥ SC nên SC ⊥ (AMN).

Bài 7.8 trang 36 SGK Toán 11 - Kết Nối Tri Thức tập 2

Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không?

Phương pháp:

Quan sát thực tế

Lời giải:

Khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng.

Bài 7.9 trang 36 SGK Toán 11 - Kết Nối Tri Thức tập 2

Một cột bóng rổ được dựng trên một sân phẳng. Bạn Hùng đo khoảng cách từ một điểm trên sân, cách chân cột 1 m đến một điểm trên cột, cách chân cột 1 m được kết quả là 1,5 m (H.7.27). Nếu phép đo của Hùng là chính xác thì cột có vuông góc với sân hay không? Có thể kết luận rằng cột không có phương thẳng đứng hay không?

Phương pháp:

Sử dụng định lý Pytago để kiểm tra vuông góc.

Lời giải:

Có 1² + 1² ≠ 1,5² . Do đó theo định lí Pythagore thì cột không vuông góc với mặt sân.

Do đó cột không có phương thẳng đứng.

Sachbaitap.com