Giải SGK Toán 11 Kết nối tri thức tập 2 trang 42Giải bài 7.10, 7,11, 7.12, 7.13, 7.14, 7.15 trang 42 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho hình chóp S.ABC có SA ( bot ) (ABC), Tam giác ABC vuông tại B, SA=AB=BC=a. a) Xác định hình chiếu của A trên mặt phẳng (SBC). b) Tính góc giữa SC và mặt phẳng (ABC). Bài 7.10 trang 42 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chóp S.ABC có SA \( \bot \) (ABC), tam giác ABC vuông tại B. a) Xác định hình chiếu của điểm S trên mặt phẳng (ABC). b) Xác định hình chiếu của tam giác SBC trên mặt phẳng (ABC). c) Xác định hình chiếu của tam giác SBC trên mặt phẳng (SAB). Phương pháp: Xác định hình chiếu của một điểm Lời giải:
a) Vì SA ⊥ (ABC) nên A là hình chiếu của S trên mặt phẳng (ABC). b) Có A là hình chiếu của S trên mặt phẳng (ABC), B là hình chiếu của B trên mặt phẳng (ABC), C là hình chiếu của C trên mặt phẳng (ABC). Do đó hình chiếu của tam giác SBC trên mặt phẳng (ABC) là tam giác ABC. c) Có SA ⊥ (ABC) nên SA ⊥ BC. Vì tam giác ABC vuông tại B nên AB ⊥ BC. Do AB ⊥ BC và SA ⊥ BC nên BC ⊥ (SAB), suy ra B là hình chiếu của C trên mặt phẳng (SAB). B là hình chiếu của B trên mặt phẳng (SAB), S là hình chiếu của S trên mặt phẳng (SAB). Do đó hình chiếu của tam giác SBC trên mặt phẳng (SAB) là SB. Bài 7.11 trang 42 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA \( \bot \) (ABCD) và \(SA = a\sqrt 2 .\) a) Tính góc giữa SC và mặt phẳng (ABCD). b) Tính góc giữa BD và mặt phẳng (SAC). c) Tìm hình chiếu của SB trên mặt phẳng (SAC). Phương pháp: - Góc giữa đường thẳng a với mặt phẳng (P) là góc giữa a và hình chiếu a’ của nó trên (P). - Xác định hình chiếu tại 1 điểm Lời giải:
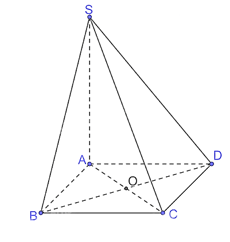
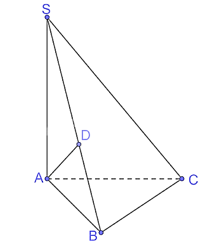
a) Vì SA ⊥ (ABCD) nên A là hình chiếu của S trên mặt phẳng (ABCD). Do đó AC là hình chiếu của SC trên mặt phẳng (ABCD). Khi đó góc giữa SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng AC và SC, mà (AC, SC) = Vì ABCD là hình vuông cạnh a nên Vì SA ⊥ (ABCD) nên SA ⊥ AC. Xét tam giác SAC vuông tại A và SA = AC = Vậy góc giữa SC và mặt phẳng (ABCD) bằng 45°. b) Vì SA ⊥ (ABCD) nên SA ⊥ BD. Do ABCD là hình vuông nên AC ⊥ BD. Vì SA ⊥ BD và AC ⊥ BD nên BD ⊥ (SAC). Do đó góc giữa BD và mặt phẳng (SAC) bằng 90°. c) Gọi O là giao điểm của AC và BD và ABCD là hình vuông, suy ra BO ⊥ AC. Mà SA ⊥ (ABCD) nên SA ⊥ BO. Vì SA ⊥ BO và BO ⊥ AC nên BO ⊥ (SAC), suy ra O là hình chiếu của B trên mặt phẳng (SAC). Có S là hình chiếu của S trên mặt phẳng (SAC). Do đó SO là hình chiếu của SB trên mặt phẳng (SAC). Bài 7.12 trang 42 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hình chópóp S.ABC có SA \( \bot \) (ABC), Tam giác ABC vuông tại B, SA=AB=BC=a a) Xác định hình chiếu của A trên mặt phẳng (SBC) b) Tính góc giữa SC và mặt phẳng (ABC). Phương pháp: - Góc giữa đường thẳng a với mặt phẳng (P) là góc giữa a và hình chiếu a’ của nó trên (P). - Xác định hình chiếu tại 1 điểm Lời giải:
a) Kẻ AD ⊥ SB tại D. Vì SA ⊥ (ABC) nên SA ⊥ BC. Do ABC là tam giác vuông tại B nên AB ⊥ BC mà SA ⊥ BC, suy ra BC ⊥ (SAB). Vì BC ⊥ (SAB) nên BC ⊥ AD mà AD ⊥ SB nên AD ⊥ (SBC). Vậy D là hình chiếu của A trên mặt phẳng (SBC). b) Vì SA ⊥ (ABC) nên AC là hình chiếu của SC trên mặt phẳng (ABC). Khi đó góc giữa SC và mặt phẳng (ABC) bằng góc giữa hai đường thẳng AC và SC, mà (AC, SC) = Xét tam giác ABC vuông tại B có: Vì SA ⊥ (ABC) nên SA ⊥ AC. Xét tam giác SAC vuông tại A, có Vậy góc giữa SC và mặt phẳng (ABC) khoảng 35,26°. Bài 7.13 trang 43 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi điểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng: a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng của chúng bằng nhau; b) Đường xiên SM lớn hơn đường xiên SM' nếu hình chiếu HM lớn hơn hình chiếu HM'. Phương pháp: Sử dụng định lí Pytago trong tam giác vuông. Lời giải:
a) Có H là hình chiếu của S trên mặt phẳng (P) nên SH ⊥ (P), suy ra SH ⊥ HM, SH ⊥ HM'. - Giả sử SM = SM'. Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2 Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2. Mà SM = SM' nên HM = HM'. - Giả sử HM = HM'. Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2 Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2. Mà HM = HM' nên SM = SM'. Vậy hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau. b) Trên tia HM lấy điểm N sao cho SN = SM' suy ra HN = HM'. Mà SM > SM' nên SM > SN ⇒ HM > HN hay HM > HM'. Bài 7.14 trang 43 SGK Toán 11 - Kết Nối Tri Thức tập 2 Trong một khoảng thời gian đầu kể từ khi cất cánh, máy bay bay theo một đường thẳng. Góc cất cánh của nó là góc giữa đường thẳng đó và mặt phẳng nằm ngang nơi cất cánh. Hai máy bay cất cánh và bay thẳng với cùng độ lớn vận tốc trong 5 phút đầu, với các góc cất cánh lần lượt là \({10^0},{15^0}.\) Hỏi sau 1 phút kể từ khi cất cánh, máy bay nào ở độ cao so với mặt đất (phẳng, nằm ngang) lớn hơn? Chú ý. Độ cao của máy bay so với mặt đất là khoảng cách từ máy bay (coi là một điểm) đến hình chiếu của nó trên mặt đất. Phương pháp: Trong tam giác vuông, tính cạnh góc vuông bằng cạnh huyền nhân sin góc đối. Lời giải:
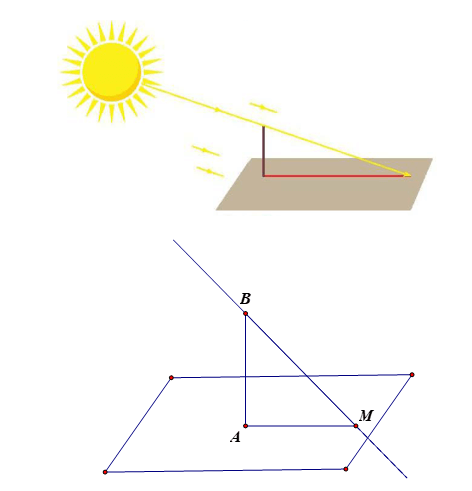
Hai máy bay có cùng độ lớn vận tốc nên sau 1 phút kể từ khi cất cánh hai máy bay bay được quãng đường bằng nhau tức AM = A'M'. Xét tam giác ABM vuông tại B có BM = AM × sin10° Xét tam giác A'CM' vuông tại C có CM' = A'M' × sin15°. Mà sin10° < sin15° nên BM < CM'. Vậy sau 1 phút cất cánh, máy bay có góc cất cánh 15° ở độ cao lớn hơn so với máy bay có góc cất cánh 10°. Bài 7.15 trang 43 SGK Toán 11 - Kết Nối Tri Thức tập 2 Hãy nêu cách đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm. Chú ý. Góc giữa đường thẳng chứa tia sáng mặt trời lúc giữa trưa với mặt phẳng nằm ngang tại vị trí đó được gọi là góc Mặt Trời. Giữa trưa là thời điểm ban ngày mà tâm Mặt Trời thuộc mặt phẳng chứa kinh tuyến đi qua điểm đang xét. Góc Mặt Trời ảnh hưởng tới sự hấp thụ nhiệt từ Mặt Trời của Trái Đất, tạo nên các mùa trong năm trên Trái Đất. Phương pháp: Sử dụng dụng cụ đo góc Lời giải:
Để đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm ta đưa về bài toán trên sân phẳng có một cây cột AB vuông góc với mặt sân, dưới ánh sáng mặt trời, bóng của cây cột trên sân AM chính là hình chiếu của cây cột. Khi đó góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang chính là góc Xét tam giác BAM vuông tại A, có: Từ đó ta tính được góc BMA. Sachbaitap.com
Xem thêm tại đây:
Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
|
-

Giải SGK Toán 11 Kết nối tri thức tập 2 trang 53
Giải bài 7.16, 7.17, 7.18, 7.19, 7.20, 7.21 trang 53 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá 1/12. Hỏi theo đó, góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá bao nhiêu độ? (Làm tròn kết quả đến chữ số thập phân thứ hai).

 Tải ngay
Tải ngay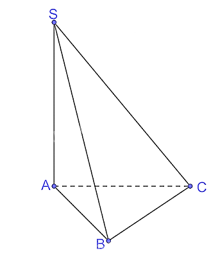
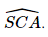
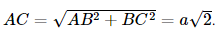 .
.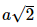 nên tam giác SAC vuông cân tại A, suy ra
nên tam giác SAC vuông cân tại A, suy ra 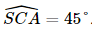
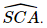 .
.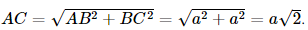
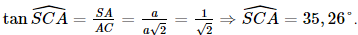
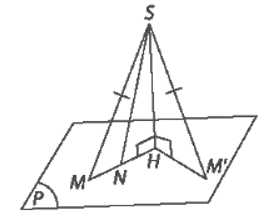

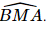 .
.