Giải SGK Toán 11 Kết nối tri thức tập 2 trang 78Giải bài 8.11, 8.12, 8.13, 8.14, 8.15 trang 78 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập. Bài 8.11 trang 78 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập. Phương pháp: Với hai biến cố A và B, nếu \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) thì A và B không độc lập. Lời giải: Hai biến cố A và B xung khắc khi và chỉ khi A ∩ B = ∅. Suy ra: P(AB) = 0. Vì P(A) > 0, P(B) > 0 nên P(A) . P(B) > 0. Do đó, P(AB) ≠ P(A) . P(B) Vậy hai biến cố A và B không độc lập. Bài 8.12 trang 78 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một thùng đựng 60 tấm thẻ cùng loại được đánh số từ 1 đến 60. Rút ngẫu nhiên một tấm thẻ trong thùng. Xét hai biến cố sau: A: “Số ghi trên tấm thẻ là ước của 60” và B: “Số ghi trên tấm thẻ là ước của 48”. Chứng tỏ rằng A và B là hai biến cố không độc lập. Phương pháp: Với hai biến cố A và B, nếu \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) thì A và B không độc lập. Lời giải: Ta có: A = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60} B = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48} Do đó, AB = A ∩ B = {1; 2; 3; 4; 6; 12}. Suy ra P(A) = Mặt khác, P(A) . P(B) = Khi đó P(AB) ≠ P(A) . P(B) nên hai biến cố A và B không độc lập. Bài 8.13 trang 78 SGK Toán 11 - Kết Nối Tri Thức tập 2 Có hai túi đựng các viên bị có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bị màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bị. Tính xác suất để: a) Hai viên bi được lấy có cùng màu xanh; b) Hai viên bi được lấy có cùng màu đỏ; c) Hai viên bi được lấy có cùng màu; d) Hai viên bi được lấy không cùng màu. Phương pháp: - Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). - Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\) - Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập. Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”; B là biến cố “Hai viên bi được lấy có cùng màu đỏ”; C là biến cố “Hai viên bi được lấy có cùng màu”. a)Xác suất lấy được viên bi màu xanh từ túi I là: Xác suất lấy được viên bi màu xanh từ túi II là: Theo quy tắc nhân, xác suất lấy được hai viên bi cùng màu xanh là: b) Xác suất lấy được viên bi màu đỏ từ túi I là: Xác suất lấy được viên bi màu đỏ từ túi II là: Theo quy tắc nhân, xác suất lấy được hai viên bi cùng màu đỏ là: P(B) = c) Ta có C = A ∪ B mà A và B xung khắc nên áp dụng công thức cộng xác suất: P(C) = P(A ∪ B) = P(A) + P(B) = Vậy xác suất để hai viên bi được lấy có cùng màu là: d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”. Khi đó, Suy ra: P(D) = 1 – P( Vậy xác suất để hai viên bi được lấy không cùng màu là Bài 8.14 trang 78 SGK Toán 11 - Kết Nối Tri Thức tập 2 Có hai túi mỗi túi đựng 10 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 10. Từ mỗi túi, lấy ngẫu nhiên ra một quả cầu. Tính xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5. Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Gọi A là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 1”, A1 là biến cố: “Quả cầu lấy ra từ túi I không ghi số 1”, A2 là biến cố: “Quả cầu lấy ra từ túi II không ghi số 1”. Ta có A = A1A2. Hai biến cố A1 và A2 độc lập nên P(A) = P(A1) . P(A2). Lại có P(A1) = P(A2) = Gọi B là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 5”, B1 là biến cố: “Quả cầu lấy ra từ túi I không ghi số 5”, B2 là biến cố: “Quả cầu lấy ra từ túi II không ghi số 5”. Ta có B = B1B2. Hai biến cố B1 và B2 độc lập nên P(B) = P(B1) . P(B2). Lại có P(B1) = P(B2) = Gọi E là biến cố: “Trong hai quả cầu lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5”. Ta có E = A ∪ B. Theo công thức cộng xác suất ta có P(E) = P(A) + P(B) – P(AB). Ta có AB là biến cố: “Hai quả cầu lấy ra không có quả nào ghi số 1 và ghi số 5”. Gọi H1 là biến cố: “Quả cầu lấy ra từ túi I không ghi số 1 và số 5”, H2 là biến cố: “Quả cầu lấy ra từ túi II không ghi số 1 và số 5”. Ta có AB = H1H2. Hai biến cố H1 và H2 độc lập nên P(AB) = P(H1) . P(H2). Lại có P(H1) = P(H2) = Do đó, P(E) = P(A) + P(B) – P(AB) = (0,9)2 + (0,9)2 – (0,8)2 = 0,98. Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là 0,98 Bài 8.15 trang 78 SGK Toán 11 - Kết Nối Tri Thức tập 2 Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để: a) Cả hai học sinh được chọn đều đạt yêu cầu; b) Cả hai học sinh được chọn đều không đạt yêu cầu; c) Chỉ có đúng một học sinh được chọn đạt yêu cầu; d) Có ít nhất một trong hai học sinh được chọn đạt yêu cầu. Phương pháp: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B). Lời giải: Xác suất để học sinh tỉnh X không đạt yêu cầu là 100% – 93% = 7% = 0,07. Xác suất để học sinh tỉnh Y không đạt yêu cầu là 100% – 87% = 13% = 0,13. Gọi A là biến cố: “Học sinh tỉnh X đạt yêu cầu”. B là biến cố: “Học sinh tỉnh Y đạt yêu cầu”. Khi đó ta có P(A) = 0,93; P(B) = 0,87; P( a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là: P(AB) = P(A) . P(B) = 0,93 . 0,87 = 0,8091. b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là: P( c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là: P(A d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là: P(A ∪ B) = P(A) + P(B) – P(AB) = 0,93 + 0,87 – 0,8091 = 0,9909. Sachbaitap.com
Xem thêm tại đây:
Bài 30. Công thức nhân xác suất cho hai biến cố độc lập
|
-

Giải SGK Toán 11 Kết nối tri thức tập 2 trang 79
Giải bài 8.16, 8.17, 8.18, 8.19, 8.20, 8.21, 8.22, 8.23, 8.24, 8.25 trang 79 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Một đoàn khách du lịch gồm 31 người, trong đó có 7 người đến từ Hà Nội, 5 người đến từ Hải Phòng. Chọn ngẫu nhiên một người trong đoàn. Tính xác suất để người đó đến từ Hà Nội hoặc đến từ Hải Phòng.

 Tải ngay
Tải ngay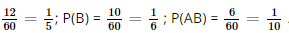 .
.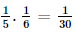 .
.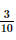 .
.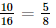 .
.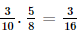

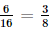 .
.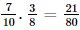
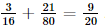 .
. .
.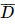 =C.
=C.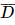 ) = 1 – P(C) = 1 –
) = 1 – P(C) = 1 – 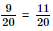 .
.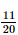
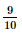
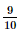 = 0,9. Do đó P(B) = (0,9)2.
= 0,9. Do đó P(B) = (0,9)2.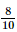 . Từ đó P(AB) = (0,8)2.
. Từ đó P(AB) = (0,8)2.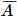 ) = 0.07; P(
) = 0.07; P(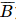 ) = 0,13 .
) = 0,13 .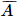
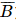 ) = P(
) = P(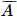 ).P(
).P(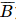 ) = 0,07 . 0,13 = 0,0091.
) = 0,07 . 0,13 = 0,0091.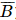 ) + P(
) + P(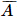 B) = 0,93 . 0,13 + 0,07 . 0,87 = 0,1818.
B) = 0,93 . 0,13 + 0,07 . 0,87 = 0,1818.