Giải SGK Toán 11 Kết nối tri thức tập 2 trang 94Giải bài 9.6, 9.7, 9.8, 9.9, 9.10, 9.11, 9.12 trang 94 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Chuyển động của một hạt trên một dây rung được cho bởi (sleft( t right) = 12 + 0,5sin left( {4pi t} right),) trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu? Bài 9.6 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính đạo hàm của các hàm số sau: a) \(y = {x^3} - 3{x^2} + 2x + 1;\) b) \(y = {x^2} - 4\sqrt x + 3.\) Phương pháp: - Sử dụng quy tắc \(\left( {u \pm v} \right)' = u' \pm v'\) - Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}};\left( {\sqrt x } \right)' = \frac{1}{{2\sqrt x }}\) Lời giải: a) y' = (x3)' – 3.(x2)' + 2.(x)' + 1' = 3x2 – 6x + 2. b) Với x > 0, ta có: y' = (x2)' – 4. Bài 9.7 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính đạo hàm của các hàm số sau: a) \(y = \frac{{2x - 1}}{{x + 2}};\) b) \(y = \frac{{2x}}{{{x^2} + 1}}.\) Phương pháp: - Sử dụng quy tắc \(\left( {u \pm v} \right)' = u' \pm v';\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) - Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) Lời giải: a) Với x ≠ – 2, ta có:
Bài 9.8 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính đạo hàm của các hàm số sau: a) \(y = x{\sin ^2}x;\) b) \(y = {\cos ^2}x + \sin 2x;\) c) \(y = \sin 3x - 3\sin x;\) d) \(y = \tan x + \cot x.\) Phương pháp: - Sử dụng quy tắc \(\left( {u \pm v} \right)' = u' \pm v';\left( {uv} \right)' = u'v + uv'\) - Sử dụng công thức \(\begin{array}{l}\left( {{x^n}} \right)' = n{x^{n - 1}};\\\left( {\sin u} \right)' = u'.\cos u;\,\\\left( {\cos x} \right)' = - \sin x\\\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}};\\\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\end{array}\) Lời giải: a) y' = (x)' . sin2x + x . (sin2x)' = sin2x + x . 2 . sinx . cosx = sin2x + xsin2x. b) y' = (cos2x)' + (sin2x)' = 2cosx.(–sinx) + 2cos2x = –2cosx.sinx + 2cos2x = –sin2x + 2cos2x. c) y' = (sin3x)' – (3sinx)' = 3cos3x – 3cosx. d) Với x≠kπ2k∈ℤ">x≠kπ2k∈ℤ">x≠k
y' = (tanx)' + (cotx)' = Bài 9.9 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Tính đạo hàm của các hàm số sau:
a) \(y = {2^{3x - {x^2}}};\) b) \(y = {\log _3}\left( {4x + 1} \right).\) Phương pháp: Sử dụng công thức \(\left( {{a^u}} \right)' = u'{a^u}\ln a;\left( {{{\log }_a}u} \right)' = \frac{{u'}}{{u\ln a}}\) Lời giải:
b) Với x> y′=log3(4x+1)= Bài 9.10 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Cho hàm số \(f\left( x \right) = 2{\sin ^2}\left( {3x - \frac{\pi }{4}} \right).\) Chứng minh rằng \(\left| {f'\left( x \right)} \right| \le 6\) với mọi x. Phương pháp: Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}};\left( {\sin u} \right)' = u'.\cos u\) Lời giải: Ta có:
Vì:
⇔ –6 ≤ f'(x) ≤ 6 với mọi x. Vậy |f'(x)| ≤ 6 với mọi x. Bài 9.11 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một vật chuyển động rơi tự do có phương trình \(h\left( t \right) = 100 - 4,9{t^2},\) ở độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật: a) Tại thời điểm t = 5 giây; b) Khi vật chạm đất. Phương pháp: Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) Lời giải: Ta có: v(t) = h'(t) = –9,8t. a) Vận tốc tại thời điểm t = 5 giây là: v(5) = –9,8 . 5 = –49 (m/s). Vậy vận tốc của vật tại thời điểm t = 5s là 49 m/s. b)Khi vật chạm đất h(t) = 0, tức là 100 – 4,9t2 = 0 ⇒ t= Vậy vận tốc của vật khi chạm đất là v Ở đây, dấu âm trong các kết quả tính vận tốc thể hiện vật chuyển động thẳng đứng xuống dưới (ngược với chiều dương). Bài 9.12 trang 94 SGK Toán 11 - Kết Nối Tri Thức tập 2 Chuyển động của một hạt trên một dây rung được cho bởi \(s\left( t \right) = 12 + 0,5\sin \left( {4\pi t} \right),\) trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu? Phương pháp: - Ý nghĩa vật lí: \(v = s'\) - Sử dụng công thức \(\left( {\sin u} \right)' = u'.\cos u\) Lời giải: Vận tốc của hạt sau t giây là: v(t) = s'(t) = 0,5.(4πt)'.cos(4πt) = 2πcos(4πt) (m/s). Vì –1 ≤ cos(4πt) ≤ 1 ⇔ –2π ≤ 2πcos(4πt) ≤ 2π ⇔ –2π ≤ v(t) ≤ 2π với mọi t. Do đó vận tốc cực đại của hạt là 2π cm/s. Sachbaitap.com
Xem thêm tại đây:
Bài 32. Các quy tắc tính đạo hàm
|
-

Giải SGK Toán 11 Kết nối tri thức tập 2 trang 96
Giải bài 9.13, 9.14, 9.15, 9.16, 9.17 trang 96 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Phương trình chuyển động của một hạt được cho bởi s(t) = 10 + 0,5sin (2nt + n/5) trong đó s tính bằng centimét và t tính bằng giây. Tính gia tốc của hạt tại thời điểm t = 5 giây (làm tròn kết quả đến chữ số thập phân thứ nhất).

 Tải ngay
Tải ngay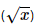 ' + 3' = 2x –
' + 3' = 2x –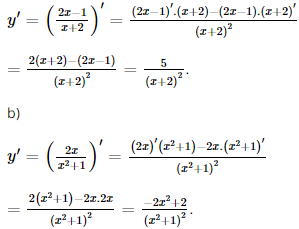
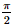 (
( 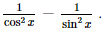
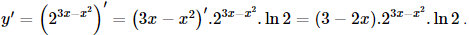
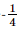
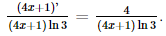
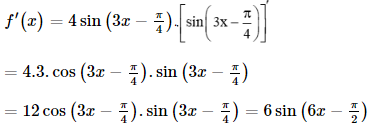
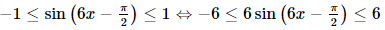
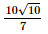
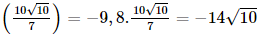 (m/s)
(m/s)