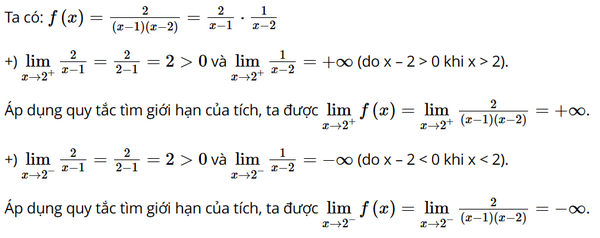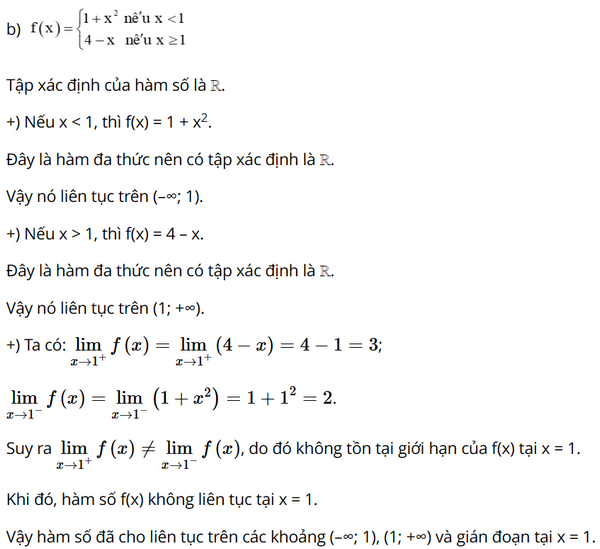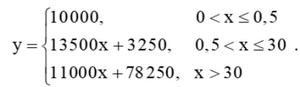Giải SGK Toán 11 trang 122 Kết Nối Tri Thức tập 1

Bài 4.14 trang 122 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục tại \(x = 1\). Biết \(f\left( 1 \right) = 2\) và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \left[ {2f\left( x \right) - g\left( x \right)} \right] = 3\). Tính \(g\left( 1 \right)\).

Phương pháp:

Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục tại điểm \({x_0}\). Khi đó:

a) Các hàm số \(y = f\left( x \right) + g\left( x \right),\;y = f\left( x \right) - g\left( x \right),\;y = f\left( x \right).g\left( x \right)\) liên tục tại \({x_0}\)

b) Hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \({x_0}\) nếu \(g\left( {{x_0}} \right) \ne 0\)

Lời giải:

Bài 4.15 trang 122 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) \(f\left( x \right) = \frac{x}{{{x^2} + 5x + 6}}\)                          

b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 + {x^2}\;,\;x < 1}\\{4 - x\;\;,\;x \ge 1}\end{array}} \right.\)

Phương pháp:

Hàm đa thức, phân thức hữu tỉ liên tục trên tập xác định của chúng.

Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {a,b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này

Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a,b} \right]\) nếu nó liên tục trên khoảng \(\left( {a,b} \right)\) và

 \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;\) \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\)

Lời giải:

Bài 4.16 trang 122 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Tìm giá trị của tham số m đề hàm số

\(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sin x\;,x \ge 0}\\{ - x + m\;\;,\;x < 0}\end{array}} \right.\)    liên tục trên \(\mathbb{R}\)

Phương pháp:

Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {a,b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này

Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a,b} \right]\) nếu nó liên tục trên khoảng \(\left( {a,b} \right)\) và

 \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;\) \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\)

Lời giải:

Tập xác định của hàm số là ℝ.

+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên (0; +∞).

+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên (–∞; 0).

Khi đó, hàm số f(x) liên tục trên các khoảng (–∞; 0) và (0; +∞).

Bài 4.17 trang 122 SGK Toán 11 tập 1 - Kết Nối Tri Thức

Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển

b) Xét tính liên tục của hàm số ở câu a.

Phương pháp:

a, Dựa vào đề bài để viết công thức hàm số.

b, Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {a,b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này

Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a,b} \right]\) nếu nó liên tục trên khoảng \(\left( {a,b} \right)\) và

 \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;\) \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\)

Lời giải:

a) Gọi x (km, x > 0) là quãng đường khách di chuyển và y (đồng) là số tiền khách phải trả theo quãng đường di chuyển x.

Với x ≤ 0,5, ta có y = 10 000.

Với 0,5 < x ≤ 30, ta có: y = 10 000 + 13 500(x – 0,5) hay y = 13 500x + 3 250.

Với x > 30, ta có: y = 10 000 + 13 500 . 29,5 + 11 000(x – 30) hay y = 11 000x + 78 250.

Vậy công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển là

b) +) Với 0 < x < 0,5 thì y = 10 000 là hàm hằng nên nó liên tục trên (0; 0,5).

+) Với 0,5 < x < 30 thì y = 13500x + 3 250 là hàm đa thức nên nó liên tục trên (0,5; 30).

+) Với x > 30 thì y = 11 000x + 78 250 là hàm đa thức nên nó liên tục trên (30; +∞).

+) Ta xét tính liên tục của hàm số tại x = 0,5 và x = 30.

- Tại x = 0,5, ta có y(0,5) = 10 000;

Sachbaitap.com