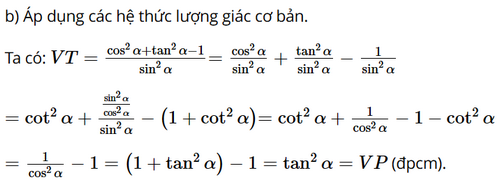Giải SGK Toán 11 trang 16 Kết Nối Tri Thức tập 1Giải bài 1.1 1.2, 1.3, 1.4, 1.5, 1.6 trang 16 SGK Toán lớp 11 Kết Nối Tri Thức tập 1. Một đường tròn có bán kinh 20 cm. Tính độ dài của các cung trên đường tròn đó có số đo sau: Bài 1.1 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Hoàn thành bảng sau:
Phương pháp: Áp dụng công thức đổi số đo độ sang radian và ngược lại. \({\alpha ^0} = \;\alpha .\frac{\pi }{{{{180}^0}}}rad\) \(\alpha \,rad = \;\alpha .{\left( {\frac{{180}}{\pi }} \right)^0}\) Lời giải:
Bài 1.2 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Một đường tròn có bán kinh 20 cm. Tính độ dài của các cung trên đường tròn đó có số đo sau: a) \(\frac{\pi }{{12}}\); b) \(1,5\); c) \({35^0}\); d) \({315^0}\). Phương pháp: Một cung của đường tròn bán kính R và có số đo \(\alpha \) rad thì có độ dài \(l = R\alpha \) Chú ý đổi từ độ sang radian Lời giải:
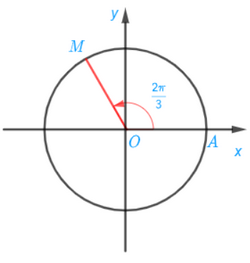
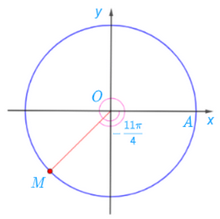
Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau: a) \(\frac{{2\pi }}{3}\); b) \( - \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( - {225^0}\). Phương pháp: Để biểu diễn các góc lượng giác trên đường tròn lượng giác ta thường sử dụng các kết quả sau - Góc \(\alpha \) và góc \(\alpha + k2\pi ,k\; \in \;\mathbb{Z}\) có cùng điểm biểu diễn trên đường tròn lượng giác. - Số điểm trên đường tròn lượng giác biểu diễn bởi số đo có dạng \(\alpha + \frac{{k2\pi }}{m}\) (với k là số nguyên và m là số nguyên dương). Từ đó để biểu diễn các góc lượng giác đó ta lần lượt cho k từ 0 tới (m – 1) rồi biểu diễn các góc đó. Lời giải:
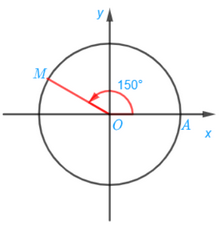
c) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 150° được xác định trong hình sau:
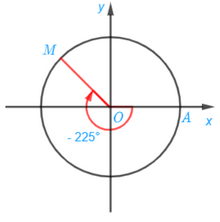
d) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng – 225° được xác định trong hình sau:
Bài 1.4 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Tính các giá trị lượng giác của góc \(\alpha \), biết: a) \(\cos \alpha = \frac{1}{5}\) và \(0 < \alpha < \frac{\pi }{2}\); b) \(\sin \alpha = \frac{2}{3}\) và \(\frac{\pi }{2} < \alpha < 2\pi \). c) \(\tan \alpha = \sqrt 5 \) và \(\pi < a < \frac{{3\pi }}{2}\); d) \(\cot \alpha = - \frac{1}{{\sqrt 2 }}\) và \(\frac{{3\pi }}{2} < \alpha < 2\pi \). Lời giải: a) Vì \(\frac{\pi }{2} < \alpha < \pi \) nên \(\cos \alpha < 0\). Mặt khác, từ \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) suy ra \(\sin \alpha = \sqrt {1 - {{\cos }^2}a} = \sqrt {1 - \frac{1}{{25}}} = \frac{{2\sqrt 6 }}{5}\) Do đó, \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{{2\sqrt 6 }}{5}}}{{\frac{1}{5}}} = 2\sqrt 6 \) và \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{\frac{1}{5}}}{{\frac{{2\sqrt 6 }}{5}}} = \frac{{\sqrt 6 }}{{12}}\) b) Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\sin \alpha > 0\). Mặt khác, từ \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) suy ra \(\cos \alpha = \sqrt {1 - {{\sin }^2}a} = \sqrt {1 - \frac{4}{9}} = \frac{{\sqrt 5 }}{3}\) Do đó, \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{2}{3}}}{{\frac{{\sqrt 5 }}{3}}} = \frac{{2\sqrt 5 }}{5}\) và \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{\frac{{\sqrt 5 }}{3}}}{{\frac{2}{3}}} = \frac{{\sqrt 5 }}{2}\) c) Ta có: \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\sqrt 5 }}\) Ta có: \({\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow {\cos ^2}\alpha = \frac{1}{{{{\tan }^2}\alpha + 1}} = \frac{1}{6} \Rightarrow \cos \alpha = \pm \frac{1}{{\sqrt 6 }}\) Vì \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \sin \alpha < 0\;\) và \( \tan \alpha = 3 > 0\,\,\) nên \(\,\,\cos \alpha > 0 \Rightarrow \cos \alpha = \frac{1}{{\sqrt 6 }}\) Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} \Rightarrow \sin \alpha = \tan \alpha .\cos \alpha = \sqrt 5 .\frac{1}{{\sqrt 6 }} = \sqrt {\frac{5}{6}} \) d) Vì \(\cot \alpha = - \frac{1}{{\sqrt 2 }}\;\,\) nên \(n\,\,\tan \alpha = \frac{1}{{\cot \alpha }} = - \sqrt 2 \) Ta có: \({\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow {\sin ^2}\alpha = \frac{1}{{{{\cot }^2}\alpha + 1}} = \frac{2}{3} \Rightarrow \sin \alpha = \pm \sqrt {\frac{2}{3}} \) Vì \(\frac{{3\pi }}{2} < \alpha < 2\pi \Rightarrow \sin \alpha < 0 \Rightarrow \sin \alpha = - \sqrt {\frac{2}{3}} \) Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} \Rightarrow \cos \alpha = \cot \alpha .\sin \alpha = \left( { - \frac{1}{{\sqrt 2 }}} \right).\left( { - \sqrt {\frac{2}{3}} } \right) = \frac{{\sqrt 3 }}{3}\) Bài 1.5 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Chứng minh các đẳng thức: a) \({\cos ^4}\alpha - {\sin ^4}\alpha = 2{\cos ^2}\alpha - 1\); b) \(\frac{{{{\cos }^2}\alpha + {{\tan }^2}\alpha - 1}}{{{{\sin }^2}\alpha }} = {\tan ^2}\alpha \). Phương pháp: Sử dụng các hệ thức lượng giác cơ bản, các hằng đẳng thức đáng nhớ và sử dụng giá trị lượng giác để biến đổi. Khi chứng minh một đẳng thức ta có thể biến đổi vế này thành vế kia, biến đổi tương đương. Lời giải: a) Áp dụng sin2 α + cos2 α = 1, suy ra sin2 α = 1 – cos2 α. Ta có: VT = cos4 α – sin4 α = (cos2 α)2 – (sin2 α)2 = (cos2 α + sin2 α)(cos2 α – sin2 α) = 1 . (cos2 α – sin2 α) = cos2 α – (1 – cos2 α) = 2cos2 α – 1 = VP (đpcm). Bài 1.6 trang 16 SGK Toán 11 tập 1 - Kết Nối Tri Thức Một người đi xe đạp với vận tốc không đổi, biết rằng bánh xe đạp quay được 11 vòng trong 5 giây. a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây. b) Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính của bánh xe đạp là 680 mm. Phương pháp: - Tính số vòng quay được trong 1 giây, suy ra góc mà bánh xe quay được Sử dụng công thức \(l = R\alpha \) để tính độ dài quãng đường Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Bài 1. Giá trị lượng giác của góc lượng giác
|
-

Giải SGK Toán 11 trang 21 Kết Nối Tri Thức tập 1
Giải bài 1.7 1.8, 1.9, 1.10, 1.11, 1.12, 1.13 trang 21 SGK Toán lớp 11 Kết Nối Tri Thức tập 1. Tính giá trị của các biểu thức sau:

 Tải ngay
Tải ngay