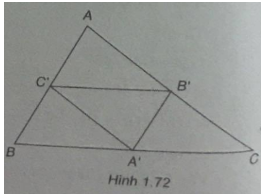
Bài 1.61 trang 46 Sách bài tập (SBT) Toán Hình học 10

Cho các điểm A'(-4;1), B'(2;4) và C'(2; - 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC.

a) Tính tọa độ các đỉnh của tam giác ABC;

b) Chứng minh rằng các trọng tâm của các tam giác ABC và A'B'C' trùng nhau.

Gợi ý làm bài

(Xem hình 1.72)

a)

\(\overrightarrow {C'A} = \overrightarrow {A'B'} = > \left\{ \matrix{
{x_A} - 2 = 6 \hfill \cr
{y_A} + 2 = 3 \hfill \cr} \right. = > \left\{ \matrix{
{x_A} = 8 \hfill \cr
{y_A} = 1 \hfill \cr} \right.\)

\(\overrightarrow {BA'} = \overrightarrow {C'B'} = > \left\{ \matrix{
- 4 - {x_B} = 0 \hfill \cr
1 - {y_B} = 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_B} = - 4 \hfill \cr
{y_B} = - 5 \hfill \cr} \right.\)

\(\overrightarrow {A'C} = \overrightarrow {C'B'} = > \left\{ \matrix{
{x_C} + 4 = 0 \hfill \cr
{y_C} - 1 = 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_C} = - 4 \hfill \cr
{y_C} = 7 \hfill \cr} \right.\)

b) Tính tọa độ trọng tâm G, G' của tam giác ABC và A'B'C' ta được G(0;1) và G'(0;1).

Vậy G=G'

Sachbaitap.net