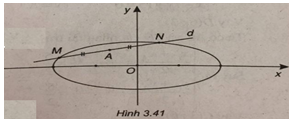
Bài 18 trang 199 Sách bài tập (SBT) Toán Hình học 10Trong mặt phẳng tọa độ Oxy, cho elip (E) Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over 4} + {y^2} = 1\) và điểm \(A\left( { - 1;{1 \over 2}} \right)\). Gọi d là đưởng thẳng đi qua A có hệ số góc là m. Xác định m để d cắt (E) tại hai điểm phân biệt M và N sao cho A là trung điểm của MN. Gợi ý làm bài (Xem hình 3.41)
Phương trình đường thẳng d có dạng \(y - {1 \over 2} = m(x + 1)\) \( \Leftrightarrow y = m(x + 1) + {1 \over 2}.\) Phương trình hoành độ giao điểm của d và (E) là : \(\eqalign{ \(\Leftrightarrow \left( {4{m^2} + 1} \right){x^2} + 4\left[ {\left( {2m + 1} \right)m} \right]x + 4{\left( {m + {1 \over 2}} \right)^2} - 4 = 0.\) A là trung điểm của MN \(\eqalign{ \( \Leftrightarrow 4{m^2} + 2m = 4{m^2} + 1 \Leftrightarrow m = {1 \over 2}.\) Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
Xem thêm tại đây:
I-Đề toán tổng hợp
|
-

Bài 21 trang 199 Sách bài tập (SBT) Toán Hình học 10
Trong mặt phẳng tọa độ Oxy, lập phương trình chính tắc của elip (E)
-

Bài 22 trang 199 Sách bài tập (SBT) Toán Hình học 10
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD

 Tải ngay
Tải ngay