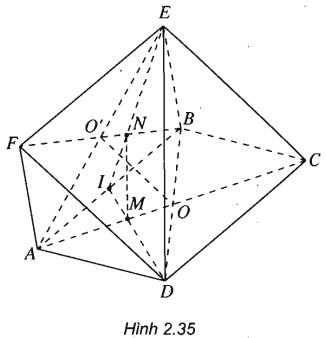
Bài 2.17 trang 74 Sách bài tập (SBT) Hình học 11Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF. Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF. a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE) b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng . Giải: (h.2.35)
a) Ta có : \(OO'\parallel DF\) ( đường trung bình của tam giác BDF). Vì \(DF \subset \left( {ADF} \right) \Rightarrow OO'\parallel \left( {ADF} \right)\). Tương tự \(OO'\parallel EC\) (đường trung bình của tam giác AEC). Vì \(EC \subset \left( {BCE} \right)\) nên \(OO'\parallel \left( {BCE} \right)\). b) Gọi I là trung điểm AB; Vì M là trọng tâm của tam giác ABD nên \(M \in DI\) Vì N là trọng tâm của tam giác ABE nên \(N \in EI\) Ta có : \(\left\{ \matrix{ Mà \(\left\{ \matrix{ Nên \(C{\rm{D}}\parallel EF\) và \(C{\rm{D = }}EF\), suy ra tứ giác CDFE là hình bình hành. \(\left\{ \matrix{ Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3. Đường thẳng và mặt phẳng song song
|
-
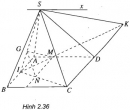
Bài 2.18 trang 74 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM
-
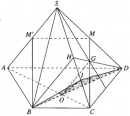
Bài 2.19 trang 74 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.
-
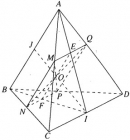
Bài 2.20 trang 74 Sách bài tập (SBT) Hình học 11
Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
-
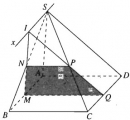
Bài 2.21 trang 75 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB

 Tải ngay
Tải ngay