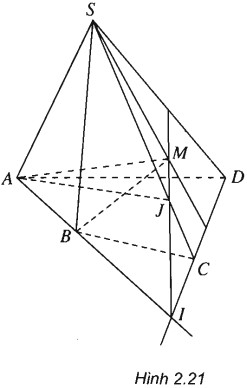
Bài 2.2 trang 66 Sách bài tập (SBT) Hình học 11Cho hình chóp S.ABCDcó đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Cho hình chóp S.ABCDcó đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng a) (SBM) và (SCD); b) (ABM) và (SCD); c) (ABM) và (SAC). Giải: (h.2.21)
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên \(\left( {SBM} \right) \cap \left( {SC{\rm{D}}} \right) = SM\). b) M là điểm chung thứ nhất của (AMB) và (SCD) Gọi \(I = AB \cap C{\rm{D}}\) Ta có: \(I \in AB \Rightarrow I \in \left( {ABM} \right)\) Mặt khác \(I \in C{\rm{D}} \Rightarrow I \in \left( {SC{\rm{D}}} \right)\) Nên \(\left( {AMB} \right) \cap \left( {SC{\rm{D}}} \right) = IM\). c) Gọi \(J = IM \cap SC\). Tacó: \(J \in SC \Rightarrow J \in \left( {SAC} \right)\) và \(J \in IM \Rightarrow J \in \left( {ABM} \right)\). Hiển nhiên \(A \in \left( {SAC} \right)\) và \(A \in \left( {ABM} \right)\) Vậy \(\left( {SAC} \right) \cap \left( {ABM} \right) = AJ\) Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 1. Đai cương về đường thằng và mặt phẳng
|
-
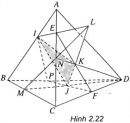
Bài 2.3 trang 66 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
-
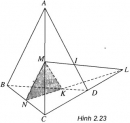
Bài 2.4 trang 66 Sách bài tập (SBT) Hình học 11
Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
-
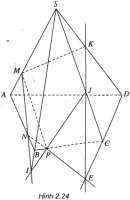
Bài 2.5 trang 67 Sách bài tập (SBT) Hình học 11
Tìm giao điểm ( nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
-
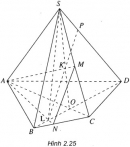
Bài 2.6 trang 67 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).

 Tải ngay
Tải ngay